Как определить проекцию на ось x. Проекции векторов на координатные оси
Пусть в пространстве даны два вектора и . Отложим от произвольной точки O
векторы и . Углом
между векторами и называется наименьший из углов . Обозначается ![]() .
.

Рассмотрим ось l и отложим на ней единичный вектор (т.е. вектор, длина которого равна единице).

Под углом между вектором и осью l понимают угол между векторами и .
Итак, пусть l – некоторая ось и – вектор.
Обозначим через A 1 и B 1 проекции на ось l соответственно точек A и B . Предположим, что A 1 имеет координату x 1 , а B 1 – координату x 2 на оси l .

Тогда проекцией вектора на ось l называется разность x 1 – x 2 между координатами проекций конца и начала вектора на эту ось.
Проекцию вектора на ось l будем обозначать .
Ясно, что если угол между вектором и осью l острый, то x 2 > x 1 , и проекция x 2 – x 1 > 0; если этот угол тупой, то x 2 < x 1 и проекция x 2 – x 1 < 0. Наконец, если вектор перпендикулярен оси l , то x 2 = x 1 и x 2 – x 1 =0.

Таким образом, проекция вектора на ось l – это длина отрезка A 1 B 1 , взятая с определённым знаком. Следовательно, проекция вектора на ось это число или скаляр.
Аналогично определяется проекция одного вектора на другой. В этом случае находятся проекции концов даного вектора на ту прямую, на которой лежит 2-ой вектор.
Рассмотрим некоторые основные свойства проекций .
ЛИНЕЙНО ЗАВИСИМЫЕ И ЛИНЕЙНО НЕЗАВИСИМЫЕ СИСТЕМЫ ВЕКТОРОВ
Рассмотрим несколько векторов .
Линейной комбинацией данных векторов называется любой вектор вида , где - некоторые числа. Числа называются коэффициентами линейной комбинации. Говорят также, что в этом случае линейно выражается через данные векторы , т.е. получается из них с помощью линейных действий.
Например, если даны три вектора то в качестве
их линейной комбинации можно рассматривать векторы: ![]()
Если вектор представлен как линейная комбинация каких-то векторов, то говорят, что он разложен по этим векторам.
Векторы называются линейно зависимыми
, если существуют
такие числа, не все равные нулю, что ![]() . Ясно, что заданные векторы будут линейно зависимыми,
если какой-либо из этих векторов линейно выражается через остальные.
. Ясно, что заданные векторы будут линейно зависимыми,
если какой-либо из этих векторов линейно выражается через остальные.
В противном случае, т.е. когда соотношение ![]() выполняется
только при
выполняется
только при ![]() , эти векторы называются линейно независимыми
.
, эти векторы называются линейно независимыми
.
Теорема 1. Любые два вектора линейно зависимы тогда и только тогда, когда они коллинеарны.
Доказательство :
Аналогично можно доказать следующую теорему.
Теорема 2. Три вектора линейно зависимы тогда и только тогда, когда они компланарны.
Доказательство .
БАЗИС
Базисом называется совокупность отличных от нулей линейно независимых векторов. Элементы базиса будем обозначать .
В предыдущем пункте мы видели, что два неколлинеарных вектора на плоскости линейно независимы. Поэтому согласно теореме 1, из предыдущего пункта, базисом на плоскости являются любые два неколлинеарных вектора на этой плоскости.
Аналогично в пространстве линейно независимы любые три некомпланарных вектора. Следовательно, базисом в пространстве назовём три некомпланарных вектора.
Справедливо следующее утверждение.
Теорема.
Пусть в пространстве
задан базис . Тогда любой вектор можно представить в
виде линейной комбинации ![]() , где x
, y
, z
– некоторые числа. Такое разложение единственно.
, где x
, y
, z
– некоторые числа. Такое разложение единственно.
Доказательство .
Таким образом, базис позволяет однозначно сопоставить каждому вектору
тройку чисел – коэффициенты разложения этого вектора по векторам базиса: . Верно и обратное, каждой
тройке чисел x, y, z
при помощи базиса можно сопоставить вектор, если составить
линейную комбинацию ![]() .
.
Если базис и ![]() , то числа x, y, z
называются координатами
вектора в данном базисе.
Координаты вектора обозначают .
, то числа x, y, z
называются координатами
вектора в данном базисе.
Координаты вектора обозначают .
ДЕКАРТОВА СИСТЕМА КООРДИНАТ
Пусть в пространстве задана точка O и три некомпланарных вектора .

Декартовой системой координат в пространстве (на плоскости) называется совокупность точки и базиса, т.е. совокупность точки и трёх некомпланарных векторов (2-х неколлинеарных векторов), выходящих из этой точки.
Точка O называется началом координат; прямые, проходящие через начало координат в направлении базисных векторов, называются осями координат – осью абсцисс, ординат и аппликат. Плоскости, проходящие через оси координат, называют координатными плоскостями.

Рассмотрим в выбранной системе координат произвольную точку M . Введём понятие координаты точки M . Вектор , соединяющий начало координат с точкой M . называется радиус-вектором точки M .

Вектору в выбранном базисе можно сопоставить тройку чисел – его координаты: ![]() .
.
Координаты радиус-вектора точки M . называются координатами точки M . в рассматриваемой системе координат. M(x,y,z) . Первая координата называется абсциссой, вторая – ординатой, третья – аппликатой.

Аналогично определяются декартовы координаты на плоскости. Здесь точка имеет только две координаты – абсциссу и ординату.
Легко видеть, что при заданной системе координат каждая точка имеет определённые координаты. С другой стороны, для каждой тройки чисел найдётся единственная точка, имеющая эти числа в качестве координат.
Если векторы, взятые в качестве базиса, в выбранной системе координат, имеют единичную длину и попарно перпендикулярны, то система координат называется декартовой прямоугольной.

Несложно показать, что .
Направляющие косинусы вектора полностью определяют его направление, но ничего не говорят о его длине.
Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:Пр a b = |b|cos(a,b) или
Где a b - скалярное произведение векторов , |a| - модуль вектора a .
Инструкция . Для нахождения проекции вектора Пp a b в онлайн режиме необходимо указать координаты векторов a и b . При этом вектор может быть задан на плоскости (две координаты) и в пространстве (три координаты). Полученное решение сохраняется в файле Word . Если векторы заданы через координаты точек, то необходимо использовать этот калькулятор .
Классификация проекций вектора
Виды проекций по определению проекция вектора
- Геометрическая проекция вектора AB на ось (вектор) называется вектор A"B" , начало которого A’ есть проекция начала A на ось (вектор), а конец B’ – проекция конца B на ту же ось.
- Алгебраическая проекция вектора AB на ось (вектор) называется длина вектора A"B" , взятая со знаком + или - , в зависимости от того, имеет ли вектор A"B" то же направление, что и ось (вектор).
Виды проекций по системе координат
Свойства проекции вектора
- Геометрическая проекция вектора есть вектор (имеет направление).
- Алгебраическая проекция вектора есть число.
Теоремы о проекциях вектора
Теорема 1 . Проекция суммы векторов на какую-либо ось равна проекции слагаемых векторов на ту же ось.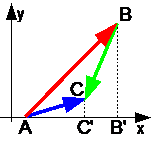 AC"
=AB"
+B"C"
AC"
=AB"
+B"C"
Теорема 2 . Алгебраическая проекция вектора на какую-либо ось равна произведению длины вектора на косинус угла между осью и вектором:
Пр a b = |b|·cos(a,b)
Виды проекций вектора
- проекция на ось OX.
- проекция на ось OY.
- проекция на вектор.
| Проекция на ось OX | Проекция на ось OY | Проекция на вектор |
Если направление вектора A’B’ совпадает с направлением оси OX, то проекция вектора A’B’ имеет положительный знак.
 | Если направление вектора A’B’ совпадает с направлением оси OY, то проекция вектора A’B’ имеет положительный знак.
 | Если направление вектора A’B’ совпадает с направлением вектора NM, то проекция вектора A’B’ имеет положительный знак.
 |
Если направление вектора противоположно с направлением оси OX, то проекция вектора A’B’ имеет отрицательный знак.
 | Если направление вектора A’B’ противоположно с направлением оси OY, то проекция вектора A’B’ имеет отрицательный знак.
| Если направление вектора A’B’ противоположно с направлением вектора NM, то проекция вектора A’B’ имеет отрицательный знак.
 |
Если вектор AB параллелен оси OX, то проекция вектора A’B’ равна модулю вектора AB.
  | Если вектор AB параллелен оси OY, то проекция вектора A’B’ равна модулю вектора AB.
  | Если вектор AB параллелен вектору NM, то проекция вектора A’B’ равна модулю вектора AB.
  |
Если вектор AB перпендикулярен оси OX, то проекция A’B’ равна нулю (нуль-вектор).
  | Если вектор AB перпендикулярен оси OY, то проекция A’B’ равна нулю (нуль-вектор).
  | Если вектор AB перпендикулярен вектору NM, то проекция A’B’ равна нулю (нуль-вектор).
  |
1. Вопрос: Может ли проекция вектора иметь отрицательный знак. Ответ: Да, проекций вектора может быть отрицательной величиной. В этом случае, вектор имеет противоположное направление (см. как направлены ось OX и вектор AB)
2. Вопрос: Может ли проекция вектора совпадать с модулем вектора. Ответ: Да, может. В этом случае, векторы параллельны (или лежат на одной прямой).
3. Вопрос: Может ли проекция вектора быть равна нулю (нуль-вектор). Ответ: Да, может. В этом случае вектор перпендикулярен соответствующей оси (вектору).
Пример 1
. Вектор (рис. 1) образует с осью OX (она задана вектором a) угол 60 о. Если OE есть единица масштаба, то |b|=4, так что ![]() .
.

Действительно, длина вектора (геометрической проекции b) равна 2, а направление совпадает с направлением оси OX.
Пример 2
. Вектор (рис. 2) образует с осью OX (с вектором a) угол (a,b) = 120 o . Длина |b| вектора b равна 4, поэтому пр a b=4·cos120 o = -2.

Действительно, длина вектора равна 2, а направление противоположно направлению оси.
Определение 1. На плоскости параллельной проекцией точки А на ось l называется точка - точка пересечения оси l с прямой, проведенной через точку А параллельно вектору, задающему направление проектирования.
Определение 2. Параллельной проекцией вектора на ось l (на вектор) называется координата вектора, относительно базиса оси l, где точки и - параллельные проекции соответственно точек А и В на ось l (рис. 1).
Согласно определению имеем
Определение 3. если и базис оси l декартов, то есть, то проекция вектора на ось l называется ортогональной (рис. 2).
В пространстве определение 2 проекции вектора на ось остается в силе, только направление проектирования задается двумя неколлинеарными векторами (рис. 3).

Из определения проекции вектора на ось вытекает, что каждая координата вектора есть проекция этого вектора на ось, определяемую соответствующим базисным вектором. При этом направление проектирования задается двумя другими базисными векторами, если проектирование ведется (рассматривается) в пространстве, или другим базисным вектором, если проектирование рассматривается на плоскости (рис. 4).

Теорема 1. Ортогональная проекция вектора на ось l равна произведению модуля вектора на косинус угла между положительным направлением оси l и, т. е.

С другой стороны
Из находим
Подставив АС в равенство (2), получим
Так как числа x и одного знака в обоих рассматриваемых случаях ((рис. 5, а) ; (рис. 5, б) , то из равенства (4) следует
Замечание. В дальнейшем мы будем рассматривать только ортогональную проекцию вектора на ось и поэтому слово «орт» (ортогональная) в обозначении будем опускать.
Приведем ряд формул, которые используются в дальнейшем при решении задач.
а)Проекция вектора на ось.
Если, то ортогональная проекция на вектор согласно формуле (5) имеет вид
в) Расстояние от точки до плоскости.

Пусть б - данная плоскость с нормальным вектором, M - данная точка,
d - расстояние от точки М до плоскости б (рис. 6).
Если N- произвольная точка плоскости б, а и - проекции точек Mи Nна ось, то
- г) Расстояние между скрещивающимися прямыми.

Пусть а и b- данные скрещивающиеся прямые, - перпендикулярный им вектор, А и В - произвольные точки прямых а и b соответственно (рис. 7), и - проекции точек Aи Bна, тогда
д) Расстояние от точки до прямой.
Пусть l - данная прямая с направляющим вектором, M - данная точка,
N - ее проекция на прямую l , тогда - искомое расстояние (рис. 8).
Если А - произвольная точка прямой l , то в прямоугольном треугольнике MNAгипотенуза MAи катет могут быть найдены. Значит,

е) Угол между прямой и плоскостью.

Пусть - направляющий вектор данной прямой l , - нормальный вектор данной плоскости б, - проекция прямой l на плоскость б (рис. 9).
Как известно, угол ц между прямой l и ее проекцией на плоскость б называется углом между прямой и плоскостью. Имеем
Приведем примеры решения метрических задач векторно-координатным методом.
По
физике
за 9 класс (И.К.Кикоин, А.К.Кикоин, 1999 год),
задача №5
к главе «ГЛАВА 1. ОБЩИЕ СВЕДЕНИЯ О ДВИЖЕНИИ
».
1. Что называют проекцией вектора на координатную ось?
1. Проекцией вектора а на координатную ось называют длину отрезка между проекциями начала и конца вектора а (перпендикулярами, опущенными из этих точек на ось) на эту координатную ось.
2. Как связан вектор перемещения тела с его координатами?
2. Проекции вектора перемещения s на оси координат равны изменению соответствующих координат тела.
3. Если координата точки с течением времени увеличивается, то какой знак имеет проекция вектора перемещения на координатную ось? А если она уменьшается?
3. Если координата точки с течением времени увеличивается, то проекция вектора перемещения на координатную ось будет положительной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора по направлению самой оси.
Если координата точки с течением времени будет уменьшаться, то проекция вектора перемещения на координатную ось будет отрицательной, т.к. в этом случае мы будем идти от проекции начала к проекции конца вектора против направляющей самой оси.
4. Если вектор перемещения параллелен оси X, то чему равен модуль проекции вектора на эту ось? А модуль проекции этого же вектора на ось У?
4. Если вектор перемещения параллелен оси Х, то модуль проекции вектора на эту ось равен модулю самого вектора, а его проекция на ось Y равна нулю.
5. Определите знаки проекций на ось X векторов перемещения, изображенных на рисунке 22. Как при этих перемещениях изменяются координаты тела?
5. Во всех нижеследующих случаях координата Y тела не изменяется, а координата Х тела будет изменяться следующим образом:
a) s 1 ;
проекция вектора s 1 , на ось Х отрицательна и по модулю равна длине вектора s 1 . При таком перемещении координата Х тела уменьшится на длину вектора s 1 .
b) s 2 ;
проекция вектора s 2 на ось X положительна и равна по модулю длине вектора s 1 . При таком перемещении координата Х тела увеличится на длину вектора s 2 .
c) s 3 ;
проекция вектора s 3 на ось Х отрицательна и равна по модулю длине вектора s 3 . При таком перемещении координата Х тела уменьшится на длину вектора s 3 .
d) s 4 ;
проекция вектора s 4 на ось X положительна и равна по модулю длине вектора s 4 . При таком перемещении координата Х тела увеличится на длину вектора s 4 .
e) s 5 ;
проекция вектора s 5 на ось Х отрицательна и равна по модулю длине вектора s 5 . При таком перемещении координата Х тела уменьшится на длину вектора s 5 .
6. Если значение пройденного пути велико, то может ли модуль перемещения быть малым?
6. Может. Это связано с тем, что перемещение (вектор перемещения) является векторной величиной, т.е. представляет собой направленный отрезок прямой, соединяющий начальное положение тела с его последующими положениями. А конечное положение тела (вне зависимости от величины пройденного пути) может находиться как угодно близко к первоначальному положению тела. В случае совпадения конечного и начального положений тела, модуль перемещения будет равен нулю.
7. Почему в механике более важен вектор перемещения тела, чем пройденный им путь?
7. Основной задачей механики является определение положения тела в любой момент времени. Зная вектор перемещения тела мы можем определить координаты тела, т.е. положение тела в любой момент времени, а зная только пройденный путь мы не можем определить координаты тела, т.к. мы не имеем сведений о направлении движения, а можем только судить о длине пройденного пути на данный момент времени.
Пусть в пространстве задана ось l, т. е. направленная прямая.
Проекцией точки М на ось l называется основание М 1 перпендикуляра ММ 1 , опущенного из точки на ось.
Точка М 1 есть точка пересечения оси l с плоскостью, проходящей через точку М перпендикулярно оси (см. рис. 7).
Если точка М лежит на оси l, то проекция точки М на ось совпадает с М1.
Пусть АВ - произвольный вектор (АВ¹ 0). Обозначим через А 1 и b 1 проекции на ось l соответственно начала А и конца В вектора АВ и рассмотрим векторА 1 В 1
Проекцией вектора АВ на ось l называет ся положительное число |A 1 B 1 | , есливектор А 1 В 1 и ось l одинаково направлены и отрица тельное число - |A 1 B 1 | , если вектор А 1 В 1 и ось l противоположно направлены (см. рис. 8). Если точки a 1 и b 1 совпадают (А 1 В 1 =0), то проекция вектора АВ равна 0.
Проекция вектора АВ на ось l обозначается так: пр l АВ. Если АВ=0 или АВ^l , то пр l АВ=0.
Угол j между вектором а и осью l (или угол между двумя векторами) изображен на рисунке 9. Очевидно,0£j£p
Рассмотрим некоторые основные свойства проекций.
Свойство 1. Проекция вектора a на ось l равна произведению модуля вектора aна косинус угла j между вектором и осью, т. е. пр l a =|a | cos j .
Следствие 5.1. Проекция вектора на ось положительна (отрицательна), есливектор образует с осью острый (тупой) угол, и равна нулю, если этот угол - прямой.
Следствие 5.2. Проекции равных векторов на одну и ту же ось равны между собой.
Свойство 2. Проекция суммы нескольких векторов на одну и ту же ось равна сумме их проекций на эту ось
Свойство 3. При умножении вектора а на число А его проекция на ось также умножается на это число, т. е.
Таким образом, линейные операции над векторами приводят к соответствующим линейным операциям над проекциями этих векторов.
5.4. Разложение вектора по ортам координатных осей.
Модуль вектора. Направляющие косинусы.
Рассмотрим в пространстве прямоугольную систему координат Oxyz. Выделим на координатных осях Ох, Оу и Oz единичные векторы (орты), обозначаемые i, j , k соответственно (см. рис. 12).
Выберем произвольный вектор а пространства и совместим его начало с началом координат: а=ОМ.
Найдем проекции вектора а на координатные оси. Проведем через конецвектора ОМ плоскости, параллельные координатным плоскостям. Точки пересечения этих плоскостей с осями обозначим соответственно через М 1 , М 2 и Мз.Получим прямоугольный параллелепипед, одной из диагоналей которого является вектор ОМ. Тогда пр х а=|OM 1 |, np y a = |ОМ 2 |, пр z а=|ОМз|. По определению суммы нескольких векторов находим а = ОМ 1 + M 1 N + NM.
А так как M 1 N=OM 2 , NM =ОМз, то
а=ОМ 1 + ОМ 2 + ОМ 3 (5.1)
Обозначим проекции вектора а=ОМ на оси Ох, Оу и Oz соответственно через а х, а у и a z , т.е. |OM 1 | = а х,|ОМ 2 | = а у, |ОМ 3 | = а z . Тогда из равенств (5.1) и (5.2) получаем
a=a x i+a y j+a z k (5.3)
Эта формула является основной в векторном исчислении и называетсяразложением вектора по ортам координатных осей. Числа а х, а у, a z называются координатами вектора а, т. е. координаты вектора есть его проекции на соответствующие координатные оси.
Векторное равенство (5.3) часто записывают в символическом виде: a = (a x ;a y ;a z).
Равенство b = (b x ;b y ; b z) означает, что b = b х i +b у j + b z k . Зная проекциивектора а, можно легко найти выражение для модуля вектора. На основании теоремы о длине диагонали прямоугольного параллелепипеда можно написать
т. е. модуль вектора равен квадратному корню из суммы квадратов его проекций на оси координат.
Пусть углы вектора а с осями Ох, Оу и Oz соответственно равны a,b,g. По свойству проекции вектора на ось, имеем
Или, что то же самое,
Числа называются направляющими косинусами вектора а.
Подставим выражения (5.5) в равенство (5.4), получаем
Сократив на получим соотношение
т. е. сумма квадратов направляющих косинусов ненулевого вектора равна единице.
Легко заметить, что координатами единичного вектора e являются числа
Итак, задав координаты вектора, всегда можно определить его модуль и направление, т.е. сам вектор.










