Подынтегральная функция неопределенного интеграла выглядит следующим. Первообразная и неопределенный интеграл, их свойства

​Интеграл является важной частью дифференциального исчисления. Интегралы могут быть двойные, тройные и т.д. Для нахождения площади поверхности и объема геометрических тел используются различные типы интегралов.

Неопределенный интеграл имеет вид: \(∫f (x)\, dx\) и определенный интеграла имеет вид: \(\int_a^b \! f (x)\, dx\)

Область плоскости, ограниченной графиком определенный интеграла:

Операции интегрирования обратны дифференцированию. По этой причине надо вспомнить первообразную, функцию, таблицу производных.

Функция \(F (x) = x^2\) является первообразной для функции \(f (х) = 2х\) . Функции \(f (х) = x^2+2\) и \(f (х) = x^2+7\) также является первообразными для функции \(f (х) = 2х\) . \(2\) и \(7-\) это константы, производные которых равны нулю, поэтому мы можем подставлять их сколько угодно, значение первообразной не изменится. Для записи неопределенного интеграла использует знак \(∫\) . Неопределенный интеграл - это совокупность всех первообразных функции \(f (х) = 2х\) . Операции интегрирования обратны дифференцированию. \(∫2x = x^2+C\) , где \(C\) это константа интегрирования, то есть если мы вычислим производную \(x^2\) , то получим \(2x\) , а это и есть \(∫2x\) . Легко, не правда ли? Если вы не поняли, то вам надо повторить производную функции. Теперь мы можем вывести формулу по которой мы будем вычислять интеграл: \(∫u^ndu=\frac{u^n+1} {n+1}, n ≠ -1\) . мы вычитали 1, теперь мы прибавляем 1 , n не может быть равно 0. Также существуют другие правила интегрирования для других основных функций которые надо выучить:

Решение неопределенного интеграла это обратный процесс нахождения первообразных дифференциального уравнения. Мы находим функцию, производная которой является интегралом, и не забываем добавлять "+ C" в конце.

Принципы интегрального исчесления были сформулированы независимо друг от друга Исааком Ньютоном и Готфридом Лейбницем в конце 17-го века. Бернхард Риман дал строгое математическое определение интегралов. Первым документированным систематическим методом, способным определять интегралы, является метод исчесления древнегреческого астронома Евдокса, который пытался найти площади и объемы, разбив их на бесконечное число известных площадей и объемов. Этот метод был далее разработан и использован Архимедом в 3-м веке до н. э. и использовался для расчета площадей парабол и приближения к площади круга.

Аналогичный метод был независимо разработан в Китае около 3-го века нашей эры Лю Хуэем, который использовал его, чтобы найти площадь круга. Этот метод позже был использован в 5-м веке китайскими математиками-отцом и сыном ЗУ Чунчжи и ЗУ Генгом, чтобы найти объем сферы.

Следующие значимые достижения в интегральном исчислении не появлялись до 17-го века. В это время работы Кавальери и Ферма начали закладывать основы современного исчисления.

В частности, фундаментальная теорема исчисления интегралов позволяет решать гораздо более широкий класс задач. Равным по важности является комплексная математическая структура, которую разработали Ньютон и Лейбниц. Эта структура интегралов взята непосредственно из работы Лейбница и стала современным интегральным исчислением.Исчисление было изменено Риманом , используя пределы. Впоследствии были рассмотрены более общие функции, особенно в контексте анализа Фурье, к которым определение Римана не применяется. Лебег сформулировал другое определение интеграла, основанное в теории мер (подполе реального анализа).

Современное обозначение неопределенного интеграла было введено Готфридом Лейбницем в 1675 году.

Интегралы широко используются во многих областях математики. Например, в теории вероятностей интегралы используются для определения вероятности попадания некоторой случайной величины в определенный диапазон.

Интегралы могут быть использованы для вычисления площади двумерной области, имеющей криволинейную границу, а также для вычисления объема трехмерного объекта, имеющего криволинейную границу.

Интегралы используются в физике, в таких областях, как кинематика, чтобы найти перемещение, время и скорость.

Определение первообразной.

Первообразной функции f(x) на промежутке (a; b) называется такая функция F(x) , что выполняется равенство для любого х из заданного промежутка.

Если принять во внимание тот факт, что производная от константы С равна нулю, то справедливо равенство . Таким образом, функция f(x) имеет множество первообразных F(x)+C , для произвольной константы С , причем эти первообразные отличаются друг от друга на произвольную постоянную величину.

Определение неопределенного интеграла.

Все множество первообразных функции f(x) называется неопределенным интегралом этой функции и обозначается .

Выражение называют подынтегральным выражением , а f(x) – подынтегральной функцией . Подынтегральное выражение представляет собой дифференциал функции f(x) .

Действие нахождения неизвестной функции по заданному ее дифференциалу называется неопределенным интегрированием, потому что результатом интегрирования является не одна функция F(x) , а множество ее первообразных F(x)+C .

На основании свойств производной можно сформулировать и доказать свойства неопределенного интеграла (свойства первообразной).

Промежуточные равенства первого и второго свойств неопределенного интеграла приведены для пояснения.

Для доказательства третьего и четвертого свойств достаточно найти производные от правых частей равенств:

Эти производные равны подынтегральным функциям, что и является доказательством в силу первого свойства. Оно же используется в последних переходах.

Таким образом, задача интегрирования является обратной задаче дифференцирования, причем между этими задачами очень тесная связь:

• первое свойство позволяет проводить проверку интегрирования. Чтобы проверить правильность выполненного интегрирования достаточно вычислить производную полученного результата. Если полученная в результате дифференцирования функция окажется равной подынтегральной функции, то это будет означать, что интегрирование проведено верно;
• второе свойство неопределенного интеграла позволяет по известному дифференциалу функции найти ее первообразную. На этом свойстве основано непосредственное вычисление неопределенных интегралов.

Рассмотрим пример.

Пример.

Найти первообразную функции , значение которой равно единице при х = 1 .

Решение.

Мы знаем из дифференциального исчисления, что (достаточно заглянуть в таблицу производных основных элементарных функций). Таким образом, . По второму свойству . То есть, имеем множество первообразных . При х = 1 получим значение . По условию, это значение должно быть равно единице, следовательно, С = 1 . Искомая первообразная примет вид .

Пример.

Найти неопределенный интеграл и результат проверить дифференцированием.

Решение.

По формуле синуса двойного угла из тригонометрии , поэтому

Первообразная функция и неопределённый интеграл

Факт 1. Интегрирование - действие, обратное дифференцированию, а именно, восстановление функции по известной производной этой функции. Восстановленная таким образом функция F (x ) называется первообразной для функции f (x ).

Определение 1. Функция F (x f (x ) на некотором промежутке X , если для всех значений x из этого промежутка выполняется равенство F "(x )=f (x ), то есть данная функция f (x ) является производной от первообразной функции F (x ). .

Например, функция F (x ) = sin x является первообразной для функции f (x ) = cos x на всей числовой прямой, так как при любом значении икса (sin x )" = (cos x ) .

Определение 2. Неопределённым интегралом функции f (x ) называется совокупность всех её первообразных . При этом употребляется запись

∫

f (x )dx

где знак ∫ называется знаком интеграла, функция f (x ) – подынтегральной функцией, а f (x )dx – подынтегральным выражением.

Таким образом, если F (x ) – какая-нибудь первообразная для f (x ) , то

∫

f (x )dx = F (x ) +C

где C - произвольная постоянная (константа).

Для понимания смысла множества первообразных функции как неопределённого интеграла уместна следующая аналогия. Пусть есть дверь (традиционная деревянная дверь). Её функция - "быть дверью". А из чего сделана дверь? Из дерева. Значит, множеством первообразных подынтегральной функции "быть дверью", то есть её неопределённым интегралом, является функция "быть деревом + С", где С - константа, которая в данном контексте может обозначать, например, породу дерева. Подобно тому, как дверь сделана из дерева при помощи некоторых инструментов, производная функции "сделана" из первообразной функции при помощи формулы, которую мы узнали, изучая производную .

Тогда таблица функций распространённых предметов и соответствующих им первообразных ("быть дверью" - "быть деревом", "быть ложкой" - "быть металлом" и др.) аналогична таблице основных неопределённых интегралов, которая будет приведена чуть ниже. В таблице неопределённых интегралов перечисляются распространённые функции с указанием первообразных, из которых "сделаны" эти функции. В части задач на нахождение неопределённого интеграла даны такие подынтегральные функции, которые без особых услилий могут быть проинтегрированы непосредственно, то есть по таблице неопределённых интегралов. В задачах посложнее подынтегральную функцию нужно предварительно преобразовать так, чтобы можно было использовать табличные интегралы.

Факт 2. Восстанавливая функцию как первообразную, мы должны учитывать произвольную постоянную (константу) C , а чтобы не писать список первообразной с различными константами от 1 до бесконечности, нужно записывать множество первообразных с произвольной константой C , например, так: 5x ³+С . Итак, произвольная постоянная (константа) входит в выражение первообразной, поскольку первообразная может быть функцией, например, 5x ³+4 или 5x ³+3 и при дифференцировании 4 или 3, или любая другая константа обращаются в нуль.

Поставим задачу интегрирования: для данной функции f (x ) найти такую функцию F (x ), производная которой равна f (x ).

Пример 1. Найти множество первообразных функции

Решение. Для данной функции первообразной является функция

Функция F (x ) называется первообразной для функции f (x ), если производная F (x ) равна f (x ), или, что одно и то же, дифференциал F (x ) равен f (x ) dx , т.е.

(2)

Следовательно, функция - первообразная для функции . Однако она не является единственной первообразной для . Ими служат также функции

где С – произвольная постоянная. В этом можно убедиться дифференцированием.

Таким образом, если для функции существует одна первообразная, то для неё существует бесконечное множество первообразных, отличающихся на постоянное слагаемое. Все первообразные для функции записываются в приведённом выше виде. Это вытекает из следующей теоремы.

Теорема (формальное изложение факта 2). Если F (x ) – первообразная для функции f (x ) на некотором промежутке Х , то любая другая первообразная для f (x ) на том же промежутке может быть представлена в виде F (x ) + C , где С – произвольная постоянная.

В следующем примере уже обращаемся к таблице интегралов, которая будет дана в параграфе 3, после свойств неопределённого интеграла. Делаем это до ознакомления со всей таблицей, чтобы была понятна суть вышеизложенного. А после таблицы и свойств будем пользоваться ими при интегрировании во всей полносте.

Пример 2. Найти множества первообразных функций:

Решение. Находим множества первообразных функций, из которых "сделаны" данные функции. При упоминании формул из таблицы интегралов пока просто примите, что там есть такие формулы, а полностью саму таблицу неопределённых интегралов мы изучим чуть дальше.

1) Применяя формулу (7) из таблицы интегралов при n = 3, получим

2) Используя формулу (10) из таблицы интегралов при n = 1/3, имеем

3) Так как

то по формуле (7) при n = -1/4 найдём

Под знаком интеграла пишут не саму функцию f , а её произведение на дифференциал dx . Это делается прежде всего для того, чтобы указать, по какой переменной ищется первообразная. Например,

, ;

здесь в обоих случаях подынтегральная функция равна , но её неопределённые интегралы в рассмотренных случаях оказываются различными. В первом случае эта функция рассматривается как функция от переменной x , а во втором - как функция от z .

Процесс нахождения неопределённого интеграла функции называется интегрированием этой функции.

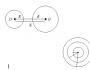
Геометрический смысл неопределённого интеграла

Пусть требуется найти кривую y=F(x) и мы уже знаем,что тангенс угла наклона касательной в каждой её точке есть заданная функция f(x) абсциссы этой точки.

Согласно геометрическому смыслу производной, тангенс угла наклона касательной в данной точке кривой y=F(x) равен значению производной F"(x) . Значит, нужно найти такую функцию F(x) , для которой F"(x)=f(x) . Требуемая в задаче функция F(x) является первообразной от f(x) . Условию задачи удовлетворяет не одна кривая, а семейство кривых. y=F(x) - одна из таких кривых, а всякая другая кривая может быть получена из неё параллельным переносом вдоль оси Oy .

Назовём график первообразной функции от f(x) интегральной кривой. Если F"(x)=f(x) , то график функции y=F(x) есть интегральная кривая.

Факт 3. Неопределённый интеграл геометрически представлен семеством всех интегральных кривых , как на рисунке ниже. Удалённость каждой кривой от начала координат определяется произвольной постоянной (константой) интегрирования C .

Свойства неопределённого интеграла

Факт 4. Теорема 1. Производная неопределённого интеграла равна подынтегральной функции, а его дифференциал – подынтегральному выражению.

Факт 5. Теорема 2. Неопределённый интеграл от дифференциала функции f (x ) равен функции f (x ) с точностью до постоянного слагаемого , т.е.

(3)

Теоремы 1 и 2 показывают, что дифференцирование и интегрирование являются взаимно-обратными операциями.

Факт 6. Теорема 3. Постоянный множитель в подынтегральном выражении можно выносить за знак неопределённого интеграла , т.е.

Функцию, восстанавливаемую по ее производной или дифференциалу, называют первообразной .

Определение. Функция F(x) называется первообразной для функции

f(x) на некотором промежутке, если в каждой точке этого промежутка

F"(x) = f(x)

или, что тоже,

dF(x) = f(x)dx

Например, F(x) = sin x является первообразной для f(x) = cos x на всей числовой оси O Х , так как

(sin x)" = cos x

Если функция F (x ) есть первообразная для функции f (x ) на [a ; b ], то функцияF (x ) + С , где C любое действительное число, также является первообразной для f (x ) при любом значении C . Действительно (F (x ) + C )" = F "(x ) + C " = f (x ).

Пример.

Определение. Если F(x) одна из первообразных для функции f(x) на [a ; b ], то выражение F(x) + С , где C произвольная постоянная, называется неопределенным интегралом от функции f (x) и обозначается символом ʃ f (x ) dx (читается: неопределенный интеграл от f(x) на dx ). Итак,

ʃ f (x ) dx = F (x ) + C ,

где f(x) называется подынтегральной функцией, f(x)dx ‒ подынтегральным выражением, x ‒ переменной интегрирования, а символ ʃ‒ знаком неопределенного интеграла.

Свойства неопределенного интеграла и его геометрические свойства.

Из определения неопределенного интеграла следует, что:

1. Производная неопределенного интеграла равна подынтегральной функции:

Действительно, F" (x ) = f (x ) и ʃ f (x ) dx = F (x ) + C . Тогда

2. Дифференциал от неопределенного интеграла равен подынтегральному выражению

Действительно,

3. Неопределенный интеграл от производной равен самой функции плюс произвольная постоянная:

Действительно, F" (x ) = f (x ). Тогда,

4. Неопределенный интеграл от дифференциала равен дифференцируемой функции плюс произвольная постоянная:

Действительно, . Тогда,

5. Постоянный множитель k (k ≠ 0) можно выносить за знак неопределенного интеграла:

6. Неопределенный интеграл от алгебраической суммы конечного числа функции равен алгебраической сумме интегралов от этих функций:

Назовем график первообразной F(x) интегральной кривой . График любой другой первообразной F(x) + C получается параллельным переносом интегральной кривой F(x) вдоль оси OY .

Пример.

Таблица основных интегралов

Основные приемы интегрирования

1. Непосредственное (табличное) интегрирование.

Непосредственное (табличное) интегрирование ‒ это приведение интеграла к табличному виду с помощью основных свойств и формул элементарной математики.

Пример 1.

Решение:

Пример 2 .

Решение:

Пример 3 .

Решение:

2. Метод подведения под дифференциал.

Пример 1.

Решение:

Пример 2 .

Решение:

Пример 3 .

Решение:

Пример 4 .

Решение:

Пример 5 .

Решение:

Пример 6 .

Решение:

Пример 7 .

Решение:

Пример 8 .

Решение:

Пример 9 .

Решение:

Пример 10 .

Решение:

3. Второй способ подведения под дифференциал.

Пример 1.

Решение:

Пример 2 .

Решение:

4. Методзамены переменной (подстановки).

Пример.

Решение:

5. Метод интегрирования по частям.

По этой формуле берутся следующие типы интегралов:

1 тип.

, формула применяется n ‒ раз, остальное dv .

2 тип.

, формула применяется один раз.

Пример 1 .

Решение:

Пример 2.

Решение:

Пример 3 .

Решение:

Пример 4 .

Решение:

ИНТЕГРИРОВАНИЕ РАЦИОНАЛЬНЫХ ДРОБЕЙ.

Рациональной дробью называется отношение двух многочленов ‒ степениm и ‒ степениn ,

Возможны следующие случаи:

1. Если , то применяют метод деления углом для исключения целой части.

2. Если и в знаменателе квадратный трехчлен, то применяют метод дополнения до полного квадрата.

Пример 1.

Решение:

Пример 2 .

Решение:

3. Метод неопределенных коэффициентов при разложении правильной рациональной дроби на сумму простейших дробей.

Любую правильную рациональную дробь , где, можно представить в виде суммы простейших дробей:

гдеA, B, C, D, E, F, M, N,… ‒ неопределенные коэффициенты.

Для нахождения неопределенных коэффициентов надо правую часть привести к общему знаменателю. Так как знаменатель совпадает со знаменателем дроби правой части, то их можно отбросить и прировнять числители. Затем, приравнивая коэффициенты при одинаковых степеняхx в левой и правой частях, получим систему линейных уравнений с n ‒ неизвестными. Решив эту систему, найдем искомые коэффициенты A , B , C , D и так далее. А, следовательно, разложим правильную рациональную дробь на простейшие дроби.

Рассмотрим на примерах возможные варианты:

1. Если множители знаменателя линейны и различны:

2. Еслисреди множителей знаменателя есть краткие множители:

3. Если среди множителей знаменателя есть квадратный трехчлен, неразложимый на множители:

Примеры: Разложить на сумму простейших рациональную дробь. Проинтегрировать.

Пример1.

Так как знаменатели дробей равны, то должны быть равны и числители, т. е.

Пример 2.

Пример 3 .

Интегральное исчисление.

Первообразная функция.

Определение: Функция F(x) называется первообразной функцией функции f(x) на отрезке , если в любой точке этого отрезка верно равенство:

Надо отметить, что первообразных для одной и той же функции может быть бесконечно много. Они будут отличаться друг от друга на некоторое постоянное число.

F 1 (x) = F 2 (x) + C.

Неопределенный интеграл.

Определение: Неопределенным интегралом функции f(x) называется совокупность первообразных функций, которые определены соотношением:

Записывают:

Условием существования неопределенного интеграла на некотором отрезке является непрерывность функции на этом отрезке.

Свойства:

1.

2.

3.

4.

Пример:

Нахождение значения неопределенного интеграла связано главным образом с нахождением первообразной функции. Для некоторых функций это достаточно сложная задача. Ниже будут рассмотрены способы нахождения неопределенных интегралов для основных классов функций – рациональных, иррациональных, тригонометрических, показательных и др.

Для удобства значения неопределенных интегралов большинства элементарных функций собраны в специальные таблицы интегралов, которые бывают иногда весьма объемными. В них включены различные наиболее часто встречающиеся комбинации функций. Но большинство представленных в этих таблицах формул являются следствиями друг друга, поэтому ниже приведем таблицу основных интегралов, с помощью которой можно получить значения неопределенных интегралов различных функций.

Методы интегрирования.

Рассмотрим три основных метода интегрирования.

Непосредственное интегрирование.

Метод непосредственного интегрирования основан на предположении о возможном значении первообразной функции с дальнейшей проверкой этого значения дифференцированием. Вообще, заметим, что дифференцирование является мощным инструментом проверки результатов интегрирования.

Рассмотрим применение этого метода на примере:

Требуется найти значение интеграла . На основе известной формулы дифференцирования
можно сделать вывод, что искомый интеграл равен
, где С – некоторое постоянное число. Однако, с другой стороны
. Таким образом, окончательно можно сделать вывод:

Заметим, что в отличие от дифференцирования, где для нахождения производной использовались четкие приемы и методы, правила нахождения производной, наконец определение производной, для интегрирования такие методы недоступны. Если при нахождении производной мы пользовались, так сказать, конструктивными методами, которые, базируясь на определенных правилах, приводили к результату, то при нахождении первообразной приходится в основном опираться на знания таблиц производных и первообразных.

Что касается метода непосредственного интегрирования, то он применим только для некоторых весьма ограниченных классов функций. Функций, для которых можно с ходу найти первообразную очень мало. Поэтому в большинстве случаев применяются способы, описанные ниже.

Способ подстановки (замены переменных).

Теорема: Если требуется найти интеграл
, но сложно отыскать первообразную, то с помощью замены x = (t) и dx = (t)dt получается:

Доказательство : Продифференцируем предлагаемое равенство:

По рассмотренному выше свойству №2 неопределенного интеграла:

f (x ) dx = f [  (t )]  (t ) dt

что с учетом введенных обозначений и является исходным предположением. Теорема доказана.

Пример. Найти неопределенный интеграл
.

Сделаем замену t = sinx , dt = cosxdt .

Пример.

Замена
Получаем:

Ниже будут рассмотрены другие примеры применения метода подстановки для различных типов функций.

Интегрирование по частям.

Способ основан на известной формуле производной произведения:

(uv) = uv + vu

где u и v – некоторые функции от х.

В дифференциальной форме: d(uv) = udv + vdu

Проинтегрировав, получаем:
, а в соответствии с приведенными выше свойствами неопределенного интеграла:

или
;

Получили формулу интегрирования по частям, которая позволяет находить интегралы многих элементарных функций.

Пример.

Как видно, последовательное применение формулы интегрирования по частям позволяет постепенно упростить функцию и привести интеграл к табличному.

Пример.

Видно, что в результате повторного применения интегрирования по частям функцию не удалось упростить к табличному виду. Однако, последний полученный интеграл ничем не отличается от исходного. Поэтому перенесем его в левую часть равенства.

Таким образом, интеграл найден вообще без применения таблиц интегралов.

Прежде чем рассмотреть подробно методы интегрирования различных классов функций, приведем еще несколько примеров нахождения неопределенных интегралов приведением их к табличным.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Пример.

Интегрирование элементарных дробей.

Определение: Элементарными называются дроби следующих четырех типов:

I.
III.

II.
IV.

m, n – натуральные числа (m  2, n  2) и b 2 – 4ac <0.

Первые два типа интегралов от элементарных дробей довольно просто приводятся к табличным подстановкой t = ax + b.

Рассмотрим метод интегрирования элементарных дробей вида III.

Интеграл дроби вида III может быть представлен в виде:

Здесь в общем виде показано приведение интеграла дроби вида III к двум табличным интегралам.

Рассмотрим применение указанной выше формулы на примерах.

Пример.

Вообще говоря, если у трехчлена ax 2 + bx + c выражение b 2 – 4ac >0, то дробь по определению не является элементарной, однако, тем не менее ее можно интегрировать указанным выше способом.

Пример .

Пример.

Рассмотрим теперь методы интегрирования простейших дробей IV типа.

Сначала рассмотрим частный случай при М = 0, N = 1.

Тогда интеграл вида
можно путем выделения в знаменателе полного квадрата представить в виде
. Сделаем следующее преобразование:

Второй интеграл, входящий в это равенство, будем брать по частям.

Обозначим:

Для исходного интеграла получаем:

Полученная формула называется рекуррентной. Если применить ее n-1 раз, то получится табличный интеграл
.

Вернемся теперь к интегралу от элементарной дроби вида IV в общем случае.

В полученном равенстве первый интеграл с помощью подстановки t = u 2 + s приводится к табличному , а ко второму интегралу применяется рассмотренная выше рекуррентная формула.

Несмотря на кажущуюся сложность интегрирования элементарной дроби вида IV, на практике его достаточно легко применять для дробей с небольшой степенью n , а универсальность и общность подхода делает возможным очень простую реализацию этого метода на ЭВМ.

Пример :

Интегрирование рациональных функций.

Интегрирование рациональных дробей.

Для того, чтобы проинтегрировать рациональную дробь необходимо разложить ее на элементарные дроби.

Теорема: Если
- правильная рациональная дробь, знаменатель P(x) которой представлен в виде произведения линейных и квадратичных множителей (отметим, что любой многочлен с действительными коэффициентами может быть представлен в таком виде: P (x ) = (x - a )  …(x - b )  (x 2 + px + q )  …(x 2 + rx + s )  ), то эта дробь может быть разложена на элементарные по следующей схеме:

где A i , B i , M i , N i , R i , S i – некоторые постоянные величины.

При интегрировании рациональных дробей прибегают к разложению исходной дроби на элементарные. Для нахождения величин A i , B i , M i , N i , R i , S i применяют так называемый метод неопределенных коэффициентов , суть которого состоит в том, что для того, чтобы два многочлена были тождественно равны, необходимо и достаточно, чтобы были равны коэффициенты при одинаковых степенях х.

Применение этого метода рассмотрим на конкретном примере.

Пример.

Приводя к общему знаменателю и приравнивая соответствующие числители, получаем:

Пример.

Т.к. дробь неправильная, то предварительно следует выделить у нее целую часть:

6x 5 – 8x 4 – 25x 3 + 20x 2 – 76x – 7 3x 3 – 4x 2 – 17x + 6

6x 5 – 8x 4 – 34x 3 + 12x 2 2x 2 + 3

9x 3 + 8x 2 – 76x - 7

9x 3 – 12x 2 – 51x +18

20x 2 – 25x – 25

Разложим знаменатель полученной дроби на множители. Видно, что при х = 3 знаменатель дроби превращается в ноль. Тогда:

3x 3 – 4x 2 – 17x + 6 x - 3

3x 3 – 9x 2 3x 2 + 5x - 2

Таким образом 3x 3 – 4x 2 – 17x + 6 = (x – 3)(3x 2 + 5x – 2) = (x – 3)(x + 2)(3x – 1). Тогда:

Для того, чтобы избежать при нахождении неопределенных коэффициентов раскрытия скобок, группировки и решения системы уравнений (которая в некоторых случаях может оказаться достаточно большой) применяют так называемый метод произвольных значений . Суть метода состоит в том, что в полученное выше выражение подставляются поочередно несколько (по числу неопределенных коэффициентов) произвольных значений х. Для упрощения вычислений принято в качестве произвольных значений принимать точки, при которых знаменатель дроби равен нулю, т.е. в нашем случае – 3, -2, 1/3. Получаем:

Окончательно получаем:

=

Пример.

Найдем неопределенные коэффициенты:

Тогда значение заданного интеграла:

Интегрирование некоторых тригонометрических

функций.

Интегралов от тригонометрических функций может быть бесконечно много. Большинство из этих интегралов вообще нельзя вычислить аналитически, поэтому рассмотрим некоторые главнейшие типы функций, которые могут быть проинтегрированы всегда.

Интеграл вида
.

Здесь R – обозначение некоторой рациональной функции от переменных sinx и cosx.

Интегралы этого вида вычисляются с помощью подстановки
. Эта подстановка позволяет преобразовать тригонометрическую функцию в рациональную.

,

Тогда

Таким образом:

Описанное выше преобразование называется универсальной тригонометрической подстановкой.

Пример.

Несомненным достоинством этой подстановки является то, что с ее помощью всегда можно преобразовать тригонометрическую функцию в рациональную и вычислить соответствующий интеграл. К недостаткам можно отнести то, что при преобразовании может получиться достаточно сложная рациональная функция, интегрирование которой займет много времени и сил.

Однако при невозможности применить более рациональную замену переменной этот метод является единственно результативным.

Пример.

Интеграл вида
если

функция R cosx .

Несмотря на возможность вычисления такого интеграла с помощью универсальной тригонометрической подстановки, рациональнее применить подстановку t = sinx .

Функция
может содержать cosx только в четных степенях, а, следовательно, может быть преобразована в рациональную функцию относительно sinx.

Пример.

Вообще говоря, для применения этого метода необходима только нечетность функции относительно косинуса, а степень синуса, входящего в функцию может быть любой, как целой, так и дробной.

Интеграл вида
если

функция R является нечетной относительно sinx .

По аналогии с рассмотренным выше случаем делается подстановка t = cosx .

Пример.

Интеграл вида

функция R четная относительно sinx и cosx .

Для преобразования функции R в рациональную используется подстановка

t = tgx.

Пример.

Интеграл произведения синусов и косинусов

различных аргументов.

В зависимости от типа произведения применятся одна из трех формул:

Пример.

Пример.

Иногда при интегрировании тригонометрических функций удобно использовать общеизвестные тригонометрические формулы для понижения порядка функций.

Пример.

Пример.

Иногда применяются некоторые нестандартные приемы.

Пример.

Интегрирование некоторых иррациональных функций.

Далеко не каждая иррациональная функция может иметь интеграл, выраженный элементарными функциями. Для нахождения интеграла от иррациональной функции следует применить подстановку, которая позволит преобразовать функцию в рациональную, интеграл от которой может быть найден как известно всегда.

Рассмотрим некоторые приемы для интегрирования различных типов иррациональных функций.

Интеграл вида
где n - натуральное число.

С помощью подстановки
функция рационализируется.

Пример.

Если в состав иррациональной функции входят корни различных степеней, то в качестве новой переменной рационально взять корень степени, равной наименьшему общему кратному степеней корней, входящих в выражение.

Проиллюстрируем это на примере.

Пример.

Интегрирование биноминальных дифференциалов.