Если существует производная то функция непрерывна. Дифференцируемость функций

СВОЙСТВА ФУНКЦИЙ, НЕПРЕРЫВНЫХ НА ОТРЕЗКЕ

Рассмотрим некоторые свойства функций непрерывных на отрезке. Эти свойства приведём без доказательства.

Функцию y = f(x) называют непрерывной на отрезке [a , b ], если она непрерывна во всех внутренних точках этого отрезка, а на его концах, т.е. в точках a и b , непрерывна соответственно справа и слева.

Теорема 1. Функция, непрерывная на отрезке [a , b ], хотя бы в одной точке этого отрезка принимает наибольшее значение и хотя бы в одной – наименьшее.

Теорема утверждает, что если функция y = f(x) непрерывна на отрезке [a , b ], то найдётся хотя бы одна точка x 1 Î [a , b ] такая, что значение функции f(x) в этой точке будет самым большим из всех ее значений на этом отрезке: f(x 1) ≥ f(x) . Аналогично найдётся такая точка x 2 , в которой значение функции будет самым маленьким из всех значений на отрезке: f(x 1) ≤ f(x) .

Ясно, что таких точек может быть и несколько, например, на рисунке показано, что функция f(x) принимает наименьшее значение в двух точках x 2 и x 2 ".

Замечание . Утверждение теоремы можно стать неверным, если рассмотреть значение функции на интервале (a , b ). Действительно, если рассмотреть функцию y = x на (0, 2), то она непрерывна на этом интервале, но не достигает в нём ни наибольшего, ни наименьшего значений: она достигает этих значений на концах интервала, но концы не принадлежат нашей области.

Также теорема перестаёт быть верной для разрывных функций. Приведите пример.

Следствие. Если функция f(x) непрерывна на [a , b ], то она ограничена на этом отрезке.

Теорема 2. Пусть функция y = f(x) непрерывна на отрезке [a , b ] и на концах этого отрезка принимает значения разных знаков, тогда внутри отрезка найдется, по крайней мере, одна точка x = C , в которой функция обращается в ноль: f(C) = 0, где a < C< b

Эта теорема имеет простой геометрический смысл: если точки графика непрерывной функции y = f(x) , соответствующие концам отрезка [a , b ] лежат по разные стороны от оси Ox , то этот график хотя бы в одной точке отрезка пересекает ось Ox . Разрывные функции этим свойством могут не обладать.

Эта теорема допускает следующее обобщение.

Теорема 3 (теорема о промежуточных значениях). Пусть функцияy = f(x) непрерывна на отрезке [a , b ] и f(a) = A , f(b) = B . Тогда для любого числа C , заключённого между A и B , найдётся внутри этого отрезка такая точка C Î [a , b ], что f(c) = C .

Эта теорема геометрически очевидна. Рассмотрим график функции y = f(x) . Пусть f(a) = A , f(b) = B . Тогда любая прямая y = C , где C – любое число, заключённое между A и B , пересечёт график функции, по крайней мере, в одной точке. Абсцисса точки пересечения и будет тем значением x = C , при котором f(c) = C .

Таким образом, непрерывная функция, переходя от одного своего значения к другому, обязательно проходит через все промежуточные значения. В частности:

Следствие. Если функция y = f(x) непрерывна на некотором интервале и принимает наибольшее и наименьшее значения, то на этом интервале она принимает, по крайней мере, один раз любое значение, заключённое между её наименьшим и наибольшим значениями.

ПРОИЗВОДНАЯ И ЕЕ ПРИЛОЖЕНИЯ. ОПРЕДЕЛЕНИЕ ПРОИЗВОДНОЙ

Пусть имеем некоторую функцию y=f(x), определенную на некотором промежутке. Для каждого значения аргумента x из этого промежутка функция y=f(x) имеет определенное значение.

Рассмотрим два значения аргумента: исходное x 0 и новое x .

Разность x– x 0 называется приращением аргумента x в точке x 0 и обозначается Δx . Таким образом, Δx = x – x 0 (приращение аргумента может быть как положительным, так и отрицательным). Из этого равенства следует, что x=x 0 +Δx , т.е. первоначальное значение переменной получило некоторое приращение. Тогда, если в точке x 0 значение функции было f(x 0 ), то в новой точке x функция будет принимать значение f(x) = f(x 0 +Δx) .

Разность y – y 0 = f(x) – f(x 0 ) называется приращением функции y = f(x) в точке x 0 и обозначается символом Δy . Таким образом,

Обычно исходное значение аргумента x 0 считается фиксированным, а новое значение x – переменным. Тогда y 0 = f(x 0 ) оказывается постоянной, а y = f(x) – переменной. Приращения Δy и Δx также будут переменными и формула (1) показывает, что Dy является функцией переменной Δx .

Составим отношение приращения функции к приращению аргумента

Найдем предел этого отношения при Δx →0. Если этот предел существует, то его называют производной данной функции f(x) в точке x 0 и обозначают f "(x 0). Итак,

Производной данной функции y = f(x) в точке x 0 называется предел отношения приращения функции Δy к приращению аргумента Δx , когда последнее произвольным образом стремится к нулю.

Заметим, что для одной и той же функции производная в различных точках x может принимать различные значения, т.е. производную можно рассматривать как функцию аргумента x . Эта функция обозначается f "(x )

Производная обозначается символами f "(x),y ", . Конкретное значение производной при x = a обозначается f "(a ) или y "| x=a .

Операция нахождения производной от функции f(x) называется дифференцированием этой функции.

Для непосредственного нахождения производной по определению можно применить следующее практическое правило :

Примеры.

МЕХАНИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Из физики известно, что закон равномерного движения имеет вид s = v·t , где s – путь, пройденный к моменту времени t , v – скорость равномерного движения.

Однако, т.к. большинство движений происходящих в природе, неравномерно, то в общем случае скорость, а, следовательно, и расстояние s будет зависеть от времени t , т.е. будет функцией времени.

Итак, пусть материальная точка движется по прямой в одном направлении по закону s=s(t).

Отметим некоторый момент времени t 0 . К этому моменту точка прошла путь s=s(t 0 ). Определим скорость v материальной точки в момент времени t 0 .

Для этого рассмотрим какой-нибудь другой момент времени t 0 + Δt . Ему соответствует пройденный путь s=s(t 0 + Δt ). Тогда за промежуток времени Δt точка прошла путь Δs=s(t 0 + Δt) –s(t).

Рассмотрим отношение . Оно называется средней скоростью в промежутке времени Δt . Средняя скорость не может точно охарактеризовать быстроту перемещения точки в момент t 0 (т.к. движение неравномерно). Для того, чтобы точнее выразить эту истинную скорость с помощью средней скорости, нужно взять меньший промежуток времени Δt .

Итак, скоростью движения в данный момент времени t 0 (мгновенной скоростью) называется предел средней скорости в промежутке от t 0 до t 0 +Δt , когда Δt →0:

,

т.е. скорость неравномерного движения это производная от пройденного пути по времени.

ГЕОМЕТРИЧЕСКИЙ СМЫСЛ ПРОИЗВОДНОЙ

Введем сначала определение касательной к кривой в данной точке.

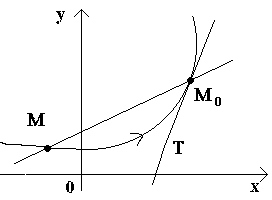
Пусть имеем кривую и на ней фиксированную точку М 0 (см. рисунок).Рассмотрим другую точку М этой кривой и проведем секущую M 0 M . Если точка М начинает перемещаться по кривой, а точка М 0 остается неподвижной, то секущая меняет свое положение. Если при неограниченном приближении точки М по кривой к точке М 0 с любой стороны секущая стремится занять положение определенной прямой М 0 Т , то прямая М 0 Т называется касательной к кривой в данной точке М 0 .

Т.о., касательной к кривой в данной точке М 0 называется предельное положение секущей М 0 М , когда точка М стремится вдоль кривой к точке М 0 .

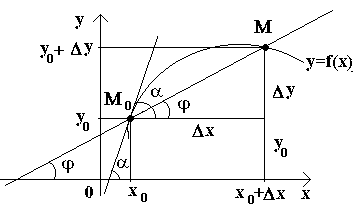
Рассмотрим теперь непрерывную функцию y=f(x) и соответствующую этой функции кривую. При некотором значении х 0 функция принимает значение y 0 =f(x 0). Этим значениям x 0 и y 0 на кривой соответствует точка М 0 (x 0 ; y 0). Дадим аргументу x 0 приращение Δх . Новому значению аргумента соответствует наращенное значение функции y 0 +Δ y=f(x 0 –Δx) . Получаем точку М(x 0 +Δx ; y 0 +Δy). Проведем секущую М 0 М и обозначим через φ угол, образованный секущей с положительным направлением оси Ox . Составим отношение и заметим, что .

Если теперь Δx →0, то в силу непрерывности функции Δу →0, и поэтому точка М , перемещаясь по кривой, неограниченно приближается к точке М 0 . Тогда секущая М 0 М будет стремиться занять положение касательной к кривой в точке М 0 , а угол φ→α при Δx →0, где через α обозначили угол между касательной и положительным направлением оси Ox . Поскольку функция tg φ непрерывно зависит от φ при φ≠π/2 то при φ→α tg φ → tg α и, следовательно, угловой коэффициент касательной будет:

т.е. f "(x) = tg α .

Т.о., геометрически у "(x 0) представляет угловой коэффициент касательной к графику этой функции в точке x 0 , т.е. при данном значении аргумента x , производная равна тангенсуугла, образованного касательной к графику функции f(x) в соответствующей точке М 0 (x; y) с положительным направлением оси Ox.

Пример. Найти угловой коэффициент касательной к кривой у = х 2 в точке М (-1; 1).

Ранее мы уже видели, что (x 2)" = 2х . Но угловой коэффициент касательной к кривой есть tg α = y "| x=-1 = – 2.

ДИФФЕРЕНЦИРУЕМОСТЬ ФУНКЦИЙ. НЕПРЕРЫВНОСТЬ ДИФФЕРЕНЦИРУЕМОЙ ФУНКЦИИ

Функция y=f(x) называется дифференцируемой в некоторой точке x 0 , если она имеет в этой точке определенную производную, т.е. если предел отношения существует и конечен.

Если функция дифференцируема в каждой точке некоторого отрезка [а ; b ] или интервала (а ; b ), то говорят, что она дифференцируема на отрезке [а ; b ] или соответственно в интервале (а ; b ).

Справедлива следующая теорема, устанавливающая связь между дифференцируемыми и непрерывными функциями.

Теорема. Если функция y=f(x) дифференцируема в некоторой точке x 0 , то она в этой точке непрерывна.

Таким образом,из дифференцируемости функции следует ее непрерывность.

Доказательство . Если , то

,

где α бесконечно малая величина, т.е. величина, стремящаяся к нулю при Δx →0. Но тогда

Δy =f "(x 0 ) Δx +αΔx => Δy →0 при Δx →0, т.е f(x) – f(x 0) →0 при x →x 0 , а это и означает, что функция f(x) непрерывна в точке x 0 . Что и требовалось доказать.

Таким образом, в точках разрыва функция не может иметь производной. Обратное утверждение неверно: существуют непрерывные функции, которые в некоторых точках не являются дифференцируемыми (т.е. не имеют в этих точках производной).

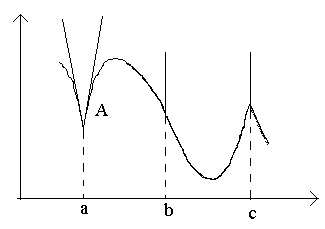
Рассмотрим на рисунке точки а, b, c.

В точке a при Δx →0 отношение не имеет предела (т.к. односторонние пределы различны при Δx →0–0 и Δx →0+0). В точке A графика нет определенной касательной, но есть две различные односторонние касательные с угловыми коэффициентами к 1 и к 2 . Такой тип точек называют угловыми точками.

В точке b при Δx →0 отношение является знакопостоянной бесконечно большой величиной . Функция имеет бесконечную производную. В этой точке график имеет вертикальную касательную. Тип точки – "точка перегиба" cвертикальной касательной.

В точке c односторонние производные являются бесконечно большими величинами разных знаков. В этой точке график имеет две слившиесявертикальные касательные. Тип – "точка возврата" с вертикальной касательной – частный случай угловой точки.

Определение: Производной от функции в точкеназывается предел, к которому стремится отношение ее приращенияв этой точке к соответствующему приращениюаргумента, когда последнее стремится к нулю:

Т.е., если определена в, то

Теорема 1:

График функции имеет невертикальную касательную тогда и только тогда, когда существует конечное значение производной этой функции в данной точке.

Доказательство:

Пусть существует значение f’()-конечное, тогда

Пусть существует невертикальная касательная => существует - конечный.

Секущая стремится к касательной.

Теорема доказана.

Билет 2 Непрерывность функции, имеющей производную.

Функция f (x), определенная в некоторой окрестности точки a, называется непрерывной в этой точке, если

Теорема: (необходимое условие существования производной)

Если функция имеет конечнуюв точке, тонепрерывна в точке.

Доказательство:

Следовательно - непрерывна в точке.

Теорема доказана.

Замечание : обратное утверждение неверно, если функция непрерывна в точке, то отсюда не следует, что она имеет производную в этой точке.

Утверждение : если функция имеет в точке правую и левую производную, то она непрерывна и справа и слева.

Билет 3

Производная суммы, произведения, частного.

Производная обратной функции.

Определение дифференцируемой функции. Необходимое и достаточное условие дифференцируемости.

Пусть функция имеет производную в точке(конечную):.

Тогда для достаточно малыхможно записать в виде суммыи некоторой функции, которую мы обозначим через, которая стремится к нулю вместе с:,

и приращение в точке может быть записано в виде:

или (1) ,

ведь выражение понимается как функция оттакая, что ее отношение кстремится к нулю вместе с.

Пояснение:

Определение .

Функция называется дифференцируемой в точке, если ее приращение можно представить в виде:(2),

где А не зависит от , но вообще зависит от.

Теорема 1:

Для того, чтобы функция была дифференцируемой в точке, необходимо и достаточно, чтобы она имела конечную производную в этой точке.

Доказательство:

Достаточность условия доказана выше: из существования конечной производной следовала возможность представленияв виде (1), где можно положить.

Необходимость условия . Пусть функция дифференцируема в точке. Тогда из (2), предполагая, получаем.

Предел правой части при существует и равен А:.

Это означает, что существует производная . Теорема доказана.

Билет 6 Дифференциал функции, его геометрический смысл.

Если функция f имеет производную f΄(x o ) в точке x o , то существует предел , где Δf=f(x o + Δx)-f(x o ) ,,или, гдеA=f΄(x o ) .

Определение:

Функция f дифференциируема в точке x o , если ее приращение представимо в виде:

Где A Δx=df . (*)

Дифференциал - это главная линейная часть приращения функции.

Если существует конечная производная f΄(x o ) в точке x o , то функция f(x) дифференцируема в этой точке.

Верно и обратное: если функция f дифференцируема в точке x o , т.е. ее приращение представимо в виде (*), то она имеет производную в точке x o , равную A :

Геометрический смысл дифференциала:

A и B – точки графика f(x) , соответствующие значениям x o и (x o + Δx) независимой переменной. Ординаты точек A и B соответственно равны f(x o ) и f(x o + Δx) . Приращение функции Δf=f(x o + Δx)-f(x o ) в точке x o равно длине отрезка BD и представимо в виде суммы Δf=BD=DC+CB , где DC=tgα Δx=f΄(x o ) Δx и α есть угол между касательной в точке A к графику и положительным направлением оси x . Отсюда видно, что DC есть дифференциал функции f в точке x o :

DC=df=f΄(x o ) Δx .

При этом на долю второго члена CB приращения Δf приходится величина . Эта величина, при больших Δx , может быть даже больше, чем главный член, но она есть бесконечно малая более высокого порядка, чем Δx , когда Δx→0 .

Содержание статьи

ПРОИЗВОДНАЯ –производной функции y = f (x ), заданной на некотором интервале (a , b ) в точке x этого интервала, называется предел, к которому стремится отношение приращения функции f в этой точке к соответствующему приращению аргумента, когда приращение аргумента стремится к нулю.

Производную принято обозначать так:

Широко употребляются и другие обозначения:

Мгновенная скорость.

Пусть точка M движется по прямой. Расстояние s движущейся точки, отсчитываемое от некоторого начального ее положения M 0 , зависит от времени t , т.е. s есть функция времени t : s = f (t ). Пусть в некоторый момент времени t движущаяся точка M находилась на расстоянии s от начального положения M 0, а в некоторый следующий момент t + Dt оказалась в положении M 1 – на расстоянии s + Ds от начального положения (см. рис .).

Таким образом, за промежуток времени Dt расстояние s изменилось на величину Ds . В этом случае говорят, что за промежуток времени Dt величина s получила приращение Ds .

Средняя скорость не может во всех случаях точно охарактеризовать быстроту перемещения точки M в момент времени t . Если, например, тело в начале промежутка Dt перемещалось очень быстро, а в конце очень медленно, то средняя скорость не сможет отразить указанных особенностей движения точки и дать представление об истинной скорости ее движения в момент t . Чтобы точнее выразить истинную скорость с помощью средней скорости, надо взять меньший промежуток времени Dt . Наиболее полно характеризует скорость движения точки в момент t тот предел, к которому стремится средняя скорость при Dt ® 0. Этот предел называют скоростью движения в данный момент:

Таким образом, скоростью движения в данный момент называется предел отношения приращения пути Ds к приращению времени Dt , когда приращение времени стремится к нулю. Так как

Геометрическое значение производной. Касательная к графику функции.

Построение касательных – одна из тех задач, которые привели к рождению дифференциального исчисления. Первый опубликованный труд, относящийся к дифференциальному исчислению и принадлежащий перу Лейбница, имел название Новый метод максимумов и минимумов, а также касательных, для которого не служат препятствием ни дробные, ни иррациональные величины, и особый для этого род исчисления .

Пусть кривая есть график функции y = f (x ) в прямоугольной системе координат (см . рис.).

При некотором значении x функция имеет значение y = f (x ). Этим значениям x и y на кривой соответствует точка M 0(x , y ). Если аргументу x дать приращение Dx , то новому значению аргумента x + Dx соответствует новое значение функции y+ Dy = f (x + Dx ). Соответствующей ему точкой кривой будет точка M 1(x + Dx , y + Dy ). Если провести секущую M 0M 1 и обозначить через j угол, образованный секущей с положительным направлением оси Ox , из рисунка непосредственно видно, что .

Если теперь Dx стремится к нулю, то точка M 1 перемещается вдоль кривой, приближаясь к точке M 0, и угол j изменяется с изменением Dx . При Dx ® 0 угол j стремится к некоторому пределу a и прямая, проходящая через точку M 0 и составляющая с положительным направлением оси абсцисс угол a, будет искомой касательной. Ее угловой коэффициент:

Следовательно, f ´(x ) = tga

т.е. значение производной f ´(x ) при данном значении аргумента x равняется тангенсу угла, образованного касательной к графику функции f (x ) в соответствующей точке M 0(x ,y ) с положительным направлением оси Ox .

Дифференцируемость функций.

Определение. Если функция y = f (x ) имеет производную в точке x = x 0, то функция дифференцируема в этой точке.

Непрерывность функции, имеющей производную. Теорема.

Если функция y = f (x ) дифференцируема в некоторой точке x = x 0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x 0 функция y = f (x ) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x | непрерывна для всех x (–Ґ х x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

Некоторые теоремы о дифференцируемых функциях. Теорема о корнях производной (теорема Ролля). Если функция f (x ) непрерывна на отрезке [a ,b ], дифференцируема во всех внутренних точках этого отрезка и на концах x = a и x = b обращается в нуль (f (a ) = f (b ) = 0), то внутри отрезка [a ,b ] существует, по крайней мере одна, точка x = с , a c b, в которой производная f ў(x ) обращается в нуль, т.е. f ў(c ) = 0.

Теорема о конечных приращениях (теорема Лагранжа). Если функция f (x ) непрерывна на отрезке [a , b ] и дифференцируема во всех внутренних точках этого отрезка, то внутри отрезка [a , b ] найдется по крайней мере одна точка с , a c b, что

f (b ) – f (a ) = f ў(c )(b – a ).

Теорема об отношении приращений двух функций (теорема Коши). Если f (x ) и g (x ) – две функции, непрерывные на отрезке [a , b ] и дифференцируемые во всех внутренних точках этого отрезка, причем g ў(x ) нигде внутри этого отрезка не обращается в нуль, то внутри отрезка [a , b ] найдется такая точка x = с , a c b, что

Производные различных порядков.

Пусть функция y = f (x ) дифференцируема на некотором отрезке [a , b ]. Значения производной f ў(x ), вообще говоря, зависят от x , т.е. производная f ў(x ) представляет собой тоже функцию от x . При дифференцировании этой функции получается так называемая вторая производная от функции f (x ), которая обозначается f ўў (x ).

Производной n- го порядка от функции f (x ) называется производная (первого порядка) от производной n- 1- го и обозначается символом y (n ) = (y (n – 1))ў.

Дифференциалы различных порядков.

Дифференциал функции y = f (x ), где x – независимая переменная, есть dy = f ў(x )dx , некоторая функция от x , но от x может зависеть только первый сомножитель f ў(x ), второй же сомножитель (dx ) является приращением независимой переменной x и от значения этой переменной не зависит. Так как dy есть функция от x , то можно определить дифференциал этой функции. Дифференциал от дифференциала функции называется вторым дифференциалом или дифференциалом второго порядка этой функции и обозначается d 2y :

d (dx ) = d 2y = f ўў(x )(dx ) 2 .

Дифференциалом n- го порядка называется первый дифференциал от дифференциала n- 1- го порядка:

d n y = d (d n –1 y ) = f (n )(x )dx (n ).

Частная производная.

Если функция зависит не от одного, а от нескольких аргументов x i (i изменяется от 1 до n , i = 1, 2,… n ), f (x 1, x 2,… x n ), то в дифференциальном исчислении вводится понятие частной производной, которая характеризует скорость изменения функции нескольких переменных, когда изменяется только один аргумент, например, x i . Частная производная 1-ого порядка по x i определяется как обычная производная, при этом предполагается, что все аргументы, кроме x i , сохраняют постоянные значения. Для частных производных вводятся обозначения

Определенные таким образом частные производные 1-ого порядка (как функции тех же аргументов) могут, в свою очередь, также иметь частные производные, это частные производные второго порядка и т.д. Взятые по разным аргументам такие производные называются смешанными. Непрерывные смешанные производные одного порядка не зависят от порядка дифференцирования и равны между собой.

Анна Чугайнова

3 Определение производной функции в точке Пусть функция f(x) определена в некоторой окрестности точки x 0. ОПРЕДЕЛЕНИЕ. Если существует (конечный) предел отношения то f(x) называется дифференцируемой точке х 0, а сам предел называется производной функции f(x) в точке х 0 и обозначается f "(x 0), то есть Обозначим x = x – x 0 – приращение аргумента при переходе из точки х 0 в точку х, а y = f(x 0 + x) – f(x 0) – соответствующее приращение функции. Тогда производная функции f(x) в точке х 0 предел отношения приращения функции к вызвавшему его приращению аргумента, когда приращение аргумента стремится к нулю.

4 Пример 1. Приведем примеры вычисления производных некоторых простейших элементарных функций, исходя из определения производной. y = a x (0 0.Считая, что | х | 0 – произвольная точка, то 0.Считая, что | х | 0 – произвольная точка, то">

0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R." title="5 Пример 3. Возьмем х 0 > 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R." class="link_thumb"> 5 5 Пример 3. Возьмем х 0 > 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R. 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R."> 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R."> 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R." title="5 Пример 3. Возьмем х 0 > 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R."> title="5 Пример 3. Возьмем х 0 > 0.Считая, что | х | 0 – произвольная точка, то Пример 4. y = sinx, x R. Возьмем х 0 R и вычислим приращение функции в этой точке: Итак (sinx) = cosx, x R.">

6 ТЕОРЕМА. Если функция f(x) дифференцируема в точке x 0, то она непрерывна в этой точке. Доказательство. Пусть существует Тогда Отсюда получим, что f (x) – f (x 0) = f "(x 0) (х – х 0) + (х – х 0)α(x) при х х 0. То есть f(x) непрерывна в точке x 0. Непрерывность дифференцируемой функции (1)

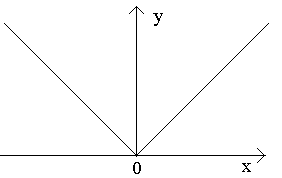
7 ЗАМЕЧАНИЕ. Непрерывность функции в точке не является достаточным условием существования в этой точке производной. Пример 5. f (x) = х. Исследуем поведение f (x) в окрестности х 0 = 0. Здесь и f (x) f (0) = 0 при x 0. Т.е. функция непрерывна в точке х 0 = 0. Рассмотрим x y 0 Предел не существует, так как Итак, функция f (x) = х не имеет производной в точке х = 0, хотя непрерывна в этой точке

8 Пример x y 0 при х 0. при х 0. Т.е. f(x) непрерывна в точке х = 0. Т.е. f(x) не имеет производной в точке х = 0 и, следовательно, не дифференцируема в этой точке. Исследуем поведение f (x) в окрестности точки х = 0.

9 Пусть функция у = f(x) дифференцируема в точке х 0. Тогда, согласно (1), ее приращение в точке х 0 можно записать в виде y = f(x 0 + x) – f(x 0) = f (x 0) х + о(x) при х. Дифференциал функции f (x 0) x – главная линейная относительно x часть приращения функции у = f(x) в точке х 0 называется дифференциалом функции в точке х 0 при приращении x и обозначается df(х 0 ; x) или df(х 0) или df или dу. y = f(x 0 + x) – f(x 0) = df(х 0 ; x) + о(x) при х. ОПРЕДЕЛЕНИЕ. Главная часть приращения, линейная относительно х. Бесконечно малая более высокого порядка, чем х. Теперь приращение функции можно записать так:

10 ЗАМЕЧАНИЕ. Приращение х часто обозначают символом dх и называют дифференциалом независимой переменной. Таким образом, дифференциал функции в точке x 0 можно записать в виде df(х 0) = f "(x 0) dх. Если функция дифференцируема в каждой точке некоторого интервала, то ее дифференциал dy – функция от х и dx: dy = f "(x) dx. Отсюда, в частности, получается выражение для производной То есть производную можно рассматривать как отношение дифференциала функции к дифференциалу независимой переменной.

11 Геометрический смысл производной и дифференциала Пусть функция у = f(x) определена в U(x 0) и дифференцируема в точке х 0. М0М0 М x0x0 x 0 + x y x y = f(x) y0y0 y 0 + у 0 L – секущая L 0 – касательная x y = f(x 0 + x) – f(x 0) при х в силу непрерывности функции. Касательной к графику функции у = f(x) в точке М 0 называется предельное положение секущей L при х. y Если функция дифференцируема в точке х 0, то в уравнении секущей у/ х f (x 0) при х и уравнение касательной имеет вид у = у 0 + f (x 0) (х – х 0).

12 М0М0 М x0x0 x 0 + x dy = df(х 0 ; x) = f (x 0) x x y = f(x) f(x0)f(x0) f(x 0 + x) 0 x y F E EM = o(x) при x 0 L0L0 tg = f (x 0) Если же у/ х при х, то прямая х = х 0, получающаяся из уравнения секущей, называется вертикальной касательной к графику функции в точке М 0. Из уравнения касательной получим у – у 0 = f (x 0) (х – х 0) = df(х 0) – приращение ординаты касательной при переходе из точки х 0 в точку х. Нормалью к графику функции в точке М 0 называется прямая, перпендикулярная касательной, проходящая через точку М 0. Ее уравнение имеет вид у = у 0 – 1/f (x 0) (х – х 0). L 1 – нормаль

13 Физические приложения производной и дифференциала Если S(t) – путь, пройденный материальной точкой за время t, то S "(t) – мгновенная скорость материальной точки, а dS = S "(t)dt – расстояние, которое прошла бы материальная точка за промежуток времени от t до t + dt, если бы она двигалась со скоростью, равной мгновенной скорости в момент t. Если Q(t) – количество электричества, протекающего через поперечное сечение проводника в момент времени t, то Q "(t) = I – сила тока. Если N(t) – количество вещества, образующегося в момент t в ходе химической реакции, то N "(t) – скорость химической реакции.

Теорема: Если функция y = f (x ) дифференцируема в некоторой точке x = x 0, то она в этой точке непрерывна.

Таким образом, в точках разрыва функция не может иметь производной. Обратное заключение неверно, т.е. из того, что в какой-нибудь точке x = x 0 функция y = f (x ) непрерывна не следует, что она в этой точке дифференцируема. Например, функция y = |x | непрерывна для всех x (–Ґ< х < Ґ), но в точке x = 0 не имеет производной. В этой точке не существует касательной к графику. Есть правая касательная и левая, но они не совпадают.

Производная сложной функции

Теорема: Пусть функция , определенная и непрерывная в окрестности , имеет производную в точке . Функция определена и непрерывна в окрестности , где , и имеет производную в точке . Тогда сложная функция имеет производную в точке и

.

где и - б.м.ф. Тогда

и , где б.м.ф. в точке .

28. Производная суммы, произведения и частного двух функций.

Производная суммы (разности) функций

Производная алгебраической суммы функций выражается следующей теоремой.

Производная суммы (разности) двух дифференцируемых функций равна сумме (разности) производных этих функций:

Производная конечной алгебраической суммы дифференцируемых функций равна такой же алгебраической сумме производных слагаемых. Например,

Производная произведения функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда произведение функций u(x)v(x) также дифференцируемо и

Производная произведения двух функций не равана произведению производных этих функций.

Производная частного функций.

Пусть u(x) и u(x) - дифференцируемые функции. Тогда, если v(x) ≠ 0 , то производная частного этих функций вычисляется по формуле

29. Производная обратной функции. Производная функции, заданной параметрически.

ТЕОРЕМА (производная обратной функции)

Пусть непрерывная, строго монотонная (возрастающая или убывающая) функция на отрезке и имеющая в точке производную . Тогда обратная функция имеет производную в точке и

.

ДОК.

= .

Теорема. (производная функции, заданной параметрически) Пусть функция x = φ(t) имеет обратную функцию t = Ф(x). Если функцииx=φ(t) , y = ψ(t) дифференцируемы и φ"(t) ≠ 0 , тогда

Доказательство

Так как функция x = φ(t) имеет обратную функцию, то формально y можно выразить черезx : y = ψ(Ф (x)) . Так как функция x = φ(t) дифференцируема, то, по теореме 5 , функция t = Ф(x) также дифференцируема.

Используя правила дифференцирования, получаем чтд

Аналогичную формулу можно получить и для второй производной y"" x :

Окончательно получаем

30. Производные высших порядков. Формула Лейбница.

Если f определена на интервале (a,b)®R, диф-ма в " точке xÎ(a,b) то на (a,b) возникает новая функция f’ :(a,b)®R, значение которой в точке x=f’ (x). Функция f’ сама может иметь производную (f’ )’ : на (a,b)®R она по отношению к исходной функции называется второй производной от f и обозначается f” (x), d 2 f(x)/dx 2 или f” xx (x), f” x 2 (x); Опр . Если определена производная f (n -1) (x) порядка n-1 от f то производная порядка n определяется формулой f (n) (x)=(f n -1))’(x). Для нее принято обозначение f (n) (x)=d n f(x)/dx n – ф-ла Лейбница , f (0) (x):=f(x).

31. Понятие дифференцируемости функции и первого дифференциала. Необходимое и достаточное условие дифференцируемости.

1.Дифференциалом функции y = f(x) называется главная линейная относительно D x часть приращения D y, равная произведению производной на приращение независимой переменной

dy = f" (x )D x.

Заметим, что дифференциал независимой переменной равен приращению этой переменной dx = D x. Поэтому формулу для дифференциала принято записывать в следующем виде:

2. Дифференцируемость. Функция называется дифференцируемой в точке x, если ее приращение ∆y в этой точке может быть представлено в виде: ∆y=A∆x + α(∆x) ∆x, где A не зависит от ∆x, α и α(∆x) – бесконечно малая функция относительно ∆x при ∆x→0.

32. Геометрический смысл производной и дифференциала. Касательная и нормаль к графику.

Пусть f определена на (a,b) и непрерывна в точке x 0 Î(a,b), пусть y 0 =f(x 0), M 0 (x 0 ,y 0); x 0 +DxÎ(a,b), Dy=f(x 0 +Dx)-f(x 0), M(x 0 +Dx, y 0 +Dy). M 0 M: y=k(x-x 0)+y 0 (1),

1 )Если $ кон. предел lim D x ® 0 k(Dx)=k 0 то прямая y=k 0 (x-x 0)+y 0 (2) назыв.

(наклонной) касательной к графику f в точке (x 0 ,y 0);

2 ) Если $ бесконечный предел

lim D x ® 0 k(Dx)=¥, то прямая x=x 0 – вертикальная касательная к графику в точке (х 0 ,у 0);

При х=х 0 (2) – предельное положение (1) т.о. предельное положение секущей М 0 М

Dх®0 это касательная y=f(x) в точке х 0 , т.к. lim D x ® 0 k(Dx)=lim D x ® 0 Dy/Dx=f’ (x 0) то уравнение

касательной имеет вид y=f’ (x 0)(x-x 0)+ y 0 , где y 0 =f(x 0) (3). Из 3 получаем что производная в точке х 0 =tga, a - угол между касательной и осью Ох, первое слагаемое f’ (x 0)(x-x 0)=f’ (x 0)Dx, Dx=x-x 0 является диф-ом dy в точке х 0 Þ y-y 0 =dy т.о. дифференциал функции равен приращению ординаты касательной в соответствующей точке графика.

3 )Если lim D x ® 0 Dy/Dx=¥, то касательной является прямая х=х 0 при этом в точке х 0 бескон. производная может существовать или не существовать.

33. Инвариантность формы первого дифференциала. Дифференциалы высших порядков, неинвариантность их формы в общем случае .

Дифференциалы высших порядков . Диф-ал от диф-ла первого порядка dy=f’(x)dx функции y=f(x) (рассматриваемого только как ф-и переменной х т.е. приращение аргумента х (dx) принимается постоянным, при условии что повторное приращ-е переменной х совпадает с начальным) называется вторым диф-ом d 2 f(x):d(df(x))=d(f’(x)dx)=d(f’(x))dx=f”(x)dxdx=f”(x)dx 2 отсюда f”(x)=d 2 f(x)/dx 2 ; Опр . Диф-ом n-го порядка n=1,2… называется дифференциалом от дифференциала порядка n-1 при условии что в диф-ле берутся одни и те же приращения dx, независимого от х. d n f(x)=d(d n -1 f(x)) не трудно видеть, что d n f(x)=f (n) (x)dx n (dx n =(dx) n) Þ f (n) (x)=d n f(x)/dx n .

Неинвариантность формы дифференциала порядка выше первого

Рассмотрим случай, когда х является не независимой переменной, а функцией от другой переменной

Теперь в правой части формулы (3) от переменной u зависит не только функция f (x ), но и дифференциал dx . Следовательно

Сравнивая формулы (2) и (4), убеждаемся, что дифференциалы второго (и более высоких порядков) не обладают инвариантностью формы.

34. Экстремумы функции. Необходимые условия экстремума (теорема Ферма).

Точки экстремума

Экстре́мум - максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума . Соответственно, если достигается минимум - точка экстремума называется точкой минимума , а если максимум - точкой максимума . В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум) .

Точка x 0 называется точкой строгого локального максимума (минимума) функции f (x ), если для всех значений аргумента из некоторой достаточно малой δ - окрестности точки х 0 выполняется неравенство

f (x ) < f (x 0) (f (x ) > f (x 0))

при х ≠ x 0 .
Локальный максимум и локальный минимум объединяются общим названием экстремум. Из определения следует, что понятие экстремума носит локальный характер в том смысле, что неравенство f (x ) < f (x 0) (f (x ) > f (x 0)) может и не выполняться для всех значений х в области определения функции, а должно выполняться лишь в некоторой окрестности точки x 0 .