Обязательно прочитайте данный параграф! Параметрические уравнения, конечно, не альфа и омега пространственной геометрии, но рабочий муравей многих задач. Причём, этот вид уравнений часто применяется неожиданно, и я бы сказал, изящно.

Если известна точка , принадлежащая прямой, и направляющий вектор данной прямой, то параметрические уравнения этой прямой задаются системой :

О самом понятии параметрических уравнений я рассказывал на уроках Уравнение прямой на плоскости и Производная параметрически заданной функции .

Всё проще пареной репы, поэтому придётся приперчить задачу:

Пример 7

Решение : Прямые заданы каноническими уравнениями и на первом этапе следует найти какую-нибудь точку, принадлежащую прямой, и её направляющий вектор.

а) Из уравнений снимаем точку и направляющий вектор: . Точку можно выбрать и другую (как это сделать – рассказано выше), но лучше взять самую очевидную. Кстати, во избежание ошибок, всегда подставляйте её координаты в уравнения.

Составим параметрические уравнения данной прямой:

Удобство параметрических уравнений состоит в том, что с их помощью очень легко находить другие точки прямой. Например, найдём точку , координаты которой, скажем, соответствуют значению параметра :

Таким образом:

б) Рассмотрим канонические уравнения . Выбор точки здесь несложен, но коварен: (будьте внимательны, не перепутайте координаты!!!). Как вытащить направляющий вектор? Можно порассуждать, чему параллельна данная прямая, а можно использовать простой формальный приём: в пропорции находятся «игрек» и «зет», поэтому запишем направляющий вектор , а на оставшееся место поставим ноль: .

Составим параметрические уравнения прямой:

в) Перепишем уравнения в виде , то есть «зет» может быть любым. А если любым, то пусть, например, . Таким образом, точка принадлежит данной прямой. Для нахождения направляющего вектора используем следующий формальный приём: в исходных уравнениях находятся «икс» и «игрек», и в направляющем векторе на данных местах записываем нули : . На оставшееся место ставим единицу : . Вместо единицы подойдёт любое число, кроме нуля.

Запишем параметрические уравнения прямой:

Для тренировки:

Пример 8

Составить параметрические уравнения следующих прямых:

Решения и ответы в конце урока. Полученные вами ответы могут несколько отличаться от моих ответов, дело в том, что параметрические уравнения можно записать не единственным способом . Важно, чтобы ваши и мои направляющие векторы были коллинеарны, и ваша точка «подходила» к моим уравнениям (ну, или наоборот, моя точка к вашим уравнениям).

Как ещё можно задать прямую в пространстве? Хочется что-нибудь придумать с вектором нормали. Однако номер не пройдёт, у пространственной прямой нормальные векторы могут смотреть совершенно в разные стороны.

Ещё об одном способе уже упоминалось на уроке Уравнение плоскости и в начале этой статьи.

УГОЛ МЕЖДУ ПЛОСКОСТЯМИ

Рассмотрим две плоскости α 1 и α 2 , заданные соответственно уравнениями:

Под углом между двумя плоскостями будем понимать один из двугранных углов, образованных этими плоскостями. Очевидно, что угол между нормальными векторами и плоскостей α 1 и α 2 равен одному из указанных смежных двугранных углов или . Поэтому . Т.к. и , то

.

Пример. Определить угол между плоскостями x +2y -3z +4=0 и 2x +3y +z +8=0.

Условие параллельности двух плоскостей.

Две плоскости α 1 и α 2 параллельны тогда и только тогда, когда их нормальные векторы и параллельны, а значит .

Итак, две плоскости параллельны друг другу тогда и только тогда, когда коэффициенты при соответствующих координатах пропорциональны:

или

Условие перпендикулярности плоскостей.

Ясно, что две плоскости перпендикулярны тогда и только тогда, когда их нормальные векторы перпендикулярны, а следовательно, или .

Таким образом, .

Примеры.

ПРЯМАЯ В ПРОСТРАНСТВЕ.

ВЕКТОРНОЕ УРАВНЕНИЕ ПРЯМОЙ.

ПАРАМЕТРИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

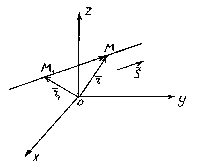
Положение прямой в пространстве вполне определяется заданием какой-либо её фиксированной точки М 1 и вектора , параллельного этой прямой.

Вектор , параллельный прямой, называется направляющим вектором этой прямой.

Итак, пусть прямая l проходит через точку М 1 (x 1 , y 1 , z 1), лежащую на прямой параллельно вектору .

Рассмотрим произвольную точку М(x,y,z) на прямой. Из рисунка видно, что .

Векторы и коллинеарны, поэтому найдётся такое число t , что , где множитель t может принимать любое числовое значение в зависимости от положения точки M на прямой. Множитель t называется параметром. Обозначив радиус-векторы точек М 1 и М соответственно через и , получаем . Это уравнение называется векторным уравнением прямой. Оно показывает, что каждому значению параметра t соответствует радиус-вектор некоторой точки М , лежащей на прямой.

Запишем это уравнение в координатной форме. Заметим, что , и отсюда

Полученные уравнения называются параметрическими уравнениями прямой.

При изменении параметра t изменяются координаты x , y и z и точка М перемещается по прямой.

КАНОНИЧЕСКИЕ УРАВНЕНИЯ ПРЯМОЙ

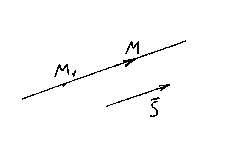
Пусть М 1 (x 1 , y 1 , z 1) – точка, лежащая на прямой l , и – её направляющий вектор. Вновь возьмём на прямой произвольную точку М(x,y,z) и рассмотрим вектор .

Ясно, что векторы и коллинеарные, поэтому их соответствующие координаты должны быть пропорциональны, следовательно,

– канонические уравнения прямой.

Замечание 1. Заметим, что канонические уравнения прямой можно было получить из параметрических,исключив параметр t . Действительно, из параметрических уравнений получаем или .

Пример. Записать уравнение прямой в параметрическом виде.

Обозначим , отсюда x = 2 + 3t , y = –1 + 2t , z = 1 –t .

Замечание 2. Пусть прямая перпендикулярна одной из координатных осей, например оси Ox . Тогда направляющий вектор прямой перпендикулярен Ox , следовательно, m =0. Следовательно, параметрические уравнения прямой примут вид

Исключая из уравнений параметр t , получим уравнения прямой в виде

Однако и в этом случае условимся формально записывать канонические уравнения прямой в виде. Таким образом, еслив знаменателе одной из дробей стоит нуль, то это означает, что прямая перпендикулярна соответствующей координатной оси.

Аналогично, каноническим уравнениям соответствует прямая перпендикулярная осям Ox и Oy или параллельная оси Oz .

Примеры.

ОБЩИЕ УРАВНЕНИЯ ПРЯМОЙ, КАК ЛИНИИ ПЕРЕСЕЧЕНИЯ ДВУХ ПЛОСКОСТЕЙ

Через каждую прямую в пространстве проходит бесчисленное множество плоскостей. Любые две из них, пересекаясь, определяют ее в пространстве. Следовательно, уравнения любых двух таких плоскостей, рассматриваемые совместно представляют собой уравнения этой прямой.

Вообще любые две не параллельные плоскости, заданные общими уравнениями

определяют прямую их пересечения. Эти уравнения называются общими уравнениями прямой.

Примеры.

Построить прямую, заданную уравнениями

Для построения прямой достаточно найти любые две ее точки. Проще всего выбрать точки пересечения прямой с координатными плоскостями. Например, точку пересечения с плоскостью xOy получим из уравнений прямой, полагая z = 0:

Решив эту систему, найдем точку M 1 (1;2;0).

Аналогично, полагая y = 0, получим точку пересечения прямой с плоскостью xOz :

От общих уравнений прямой можно перейтик её каноническим или параметрическим уравнениям. Для этого нужно найти какую-либо точку М 1 на прямой и направляющий вектор прямой.

Координаты точки М 1 получим из данной системы уравнений, придав одной из координат произвольное значение. Для отыскания направляющего вектора, заметим, что этот вектор должен быть перпендикулярен к обоим нормальным векторам и . Поэтому за направляющий вектор прямой l можно взять векторное произведение нормальных векторов:

.

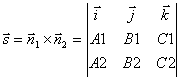Пример. Привести общие уравнения прямой к каноническому виду.

Найдём точку, лежащую на прямой. Для этого выберем произвольно одну из координат, например, y = 0 и решим систему уравнений:

Нормальные векторы плоскостей, определяющих прямую имеют координаты Поэтому направляющий вектор прямой будет

. Следовательно, l : .

УГОЛ МЕЖДУ ПРЯМЫМИ

Углом между прямыми в пространстве будем называть любой из смежных углов, образованных двумя прямыми, проведёнными через произвольную точку параллельно данным.

Пусть в пространстве заданы две прямые:

Очевидно, что за угол φ между прямыми можно принять угол между их направляющими векторами и . Так как , то по формуле для косинуса угла между векторами получим

Уравнение, которое кроме неизвестной величины содержит также другую дополнительную величину, которая может принимать различные значения из некоторой области, называется параметрическим . Эта дополнительная величина в уравнении называется параметр . На самом деле с каждым параметрическим уравнением может быть написано множество уравнений. Мы рассмотрим модуль параметрического уравнения и решение простых параметрических уравнений.

Задача 1 Решите уравнения в отношении к $x$
A) $x + a = 7$
B) $2x + 8a = 4$
C) $x + a = 2a – x$
D) $ax = 5$
E) $a – x = x + b$
F) $ax = 3a$

Решение :

A) $x + a = 7 \Leftrightarrow x = 7 – a$, то есть решение к данному уравнению найдено.
Для различных значений параметров, решения есть $x = 7 – a$

B) $2x + 8a = 4 \Leftrightarrow 2x = 4 - 8a \Leftrightarrow x = 2 – 4a$

C) $x + a = 2a – x \Leftrightarrow x + x = 2a – a \Leftrightarrow 2x = a \Leftrightarrow x = \frac{a}{2}$

D) $ax = 5$, когда а отличается от 0 мы можем разделить обе части на a и мы получим $x = 5$
Если $a = 0$, мы получим уравнение, такое как $0.x = 5$, и которое не имеет решения;

E) $a – x = x + b \Leftrightarrow a – b = x + x \Leftrightarrow 2x = a – b \Leftrightarrow x = \frac{a-b}{2}$

F) Когда a = 0 уравнение ax = 3a равно 0.x = 0
Поэтому, любое x является решением. Если a отличается от 0, тогда
$ax = 3a \Leftrightarrow x = \frac{3a}{a} \Leftrightarrow x = 3$

Задача 2 Если a является параметром, решите уравнение:
A) $(a + 1)x = 2a + 3$
B) $2a + x = ax + 4$
C) $a^2x – x = a$
D) $a^2x + x = a$

Решение :

A) Если $a + 1$ отлично от 0, то есть.. $a \neq -1$,
тогда $x = \frac{2a+3}{a+1}$;
если $a + 1 = 0$, i.e. $a = - 1$
уравнение принимает вид $0\cdot x = (2)\cdot(-1) + 3 \Leftrightarrow$
$0\cdot x = 1$, что не имеет решения;

B) $2a + x = ax + 4 \Leftrightarrow$
$x – ax = 4 - 2a \Leftrightarrow$
$(1 – a)\cdot x = 2(2 – a)$
Если $(1 – a) \neq 0$, то есть a $\neq 1$; решение будет
$x = \frac{2(2 - a)}{(1 - a)}$;
Если $a = 1$ уравнение примет вид $0\cdot x = 2(2 - 1) \Leftrightarrow$
$0\cdot x = 2$, что не имеет решения

C) $a^2x – x = a \Leftrightarrow$
$x(a^2 -1) = a \Leftrightarrow$
$(a - 1)(a + 1)x = a$
Если $a - 1 \neq 0$ и $a + 1 \neq 0$ то есть $a \neq 1, -1$,
решением есть is $x = \frac{a}{(a - 1)(a + 1)}$
Если $a = 1$ or $a = -1$, уравнение принимает вид is $0\cdot x = \pm 1$, что не имеет решения

D) $a^2x + x = a \Leftrightarrow$
$(a^2 + 1)x = a$
В этом случае $a^2 + 1 \neq 0$ для любого $а$, потому что это есть сумма позитивного числа (1) и одного негативного числа
$(a^2 \geq 0)$ поэтому $x = \frac{a}{a^2 + 1}$

Задача 3 Если a and b являются параметрами, решите уравнения:
A) $ax + b = 0$
B) $ax + 2b = x$
C) $(b - 1)y = 1 – a$
D) $(b^2 + 1)y = a + 2$

Решение :

A) $ax + b = 0 \Leftrightarrow ax = -b$
Если $a \neq 0$, тогда решение есть $x = -\frac{b}{a}$.
Если $a = 0, b \neq 0$, уравнение принимает вид $0\cdot x = -b$ и не имеет решения.
Если $a = 0$ и $b = 0$, уравнение принимает вид $0\cdot x = 0$ и любое $x$ является решением;

B) $ax + 2b = x \Leftrightarrow ax – x = -2b \Leftrightarrow (a - 1)x = -2b$
Если $a - 1 \neq 0$, i.e. $a \neq 1$, решение есть is $x = -\frac{2b}{a-1}$
Если $a - 1 = 0$, то есть $a = 1$, и $b \neq 0$, уравнение принимает вид $0\cdot x = - 2b$ и не имеет решения

C) Если $b - 1 \neq 0$, то есть $b \neq 1$,
решением есть $y = \frac{1-a}{b-1}$
Если $b - 1 = 0$, то есть $b = 1$, но $1 – a \neq 0$,
то есть $a \neq 1$, уравнение принимает вид $0\cdot y = 1 – a$ и не имеет решения.
Если $b = 1$ и $a = 1$ уравнение принимает вид $0\cdot y = 0$ и любое $y$ является решением

D) $b^2 + 1 \neq 0$ для любого $b$(почему?), поэтому
$y = \frac{a+2}{b^2}$ является решением уравнения.

Задача $4$ Для каких значений $x$ следующие выражения имеют равные значения:
A) $5x + a$ и $3ax + 4$
B) $2x - 2$ и $4x + 5a$

Решение :

Чтобы получить одинаковые значения мы должны найти решения уравнений
$5x + a = 3ax + 4$ и $2x – 2 = 4x + 5a$

A) $5x + a = 3ax + 4 \Leftrightarrow$
$5x - 3ax = 4 – a \Leftrightarrow$
$(5 - 3a)x = 4 – a$
Если $5 - 3a \neq 0$, т.e. $a \neq \frac{5}{3}$, решения есть $x = \frac{4-a}{5-3a}$
Если $5 - 3a = 0$, т.e. $a = \frac{5}{3}$, уравнение принимает вид $0\cdot x = 4 – \frac{5}{3} \Leftrightarrow$
$0\cdot x = \frac{7}{3}$, что не имеет решения

B) $2x - 2 = 4x + 5a \Leftrightarrow$
$-2 - 5a = 4x - 2x \Leftrightarrow$
$2x = - 2 - 5a \Leftrightarrow$
$x = -\frac{2+5a}{2}$

Задача 5
A) $|ax + 2| = 4$
B) $|2x + 1| = 3a$
C) $|ax + 2a| = 3$

Решение :

A) $|ax + 2| = 4 \Leftrightarrow ax + 2 = 4$ или $ax + 2 = -4 \Leftrightarrow$
$ax = 2$ или $ax = - 6$
Если $a \neq 0$, уравнения примут вид $x = \frac{2}{a}$ or $x = -\frac{6}{a}$
Если $a = 0$, уравнения не имею решения

B) Если $a Если $a > 0$, это эквивалентно $2x + 1 = 3a$
или $2x + 1 = -3a \Leftrightarrow 2x = 3a - 1 \Leftrightarrow x = \frac{3a-1}{2}$ or
$2x = -3a - 1 \Leftrightarrow x = \frac{3a-1}{2} = -\frac{3a-1}{2}$

C) $|ax + 2a| = 3 \Leftrightarrow ax + 2a = 3$ или $ax + 2a = - 3$,
и мы находим $ax = 3 - 2a$ или $ax = -3 - 2a$
Если a = 0, тогда нет решений, если $a \neq 0$
решениями есть: $x = \frac{3-2a}{a}$ и $x = -\frac{3+2a}{a}$

Задача 6 Решите уравнение $2 – x = 2b – 2ax$, где a и b являются действительными параметрами. Найдите, для каких значениях a уравнение имеет в качестве решения натуральное число, если $b = 7$

Решение :

Представим данное уравнение в следующем виде: $(2a - 1)x = 2(b - 1)$
Возможны следующие варианты:
Если $2a - 1 \neq 0$, т.e. $a \neq \frac{1}{2}$, уравнение имеет единственное решение
$x = \frac{2(b-1)}{2a-1}$
Если $a = \frac{1}{2}$ и $b = 1$, уравнение получает вид $0\cdot x = 0$ и любое $x$ является решением
Если $a = \frac{1}{2}$ и $b \neq 1$, мы получаем $0\cdot x = 2(b - 1)$, где $2(b - 1) \neq 0$
В этом случае уравнение не имеет решения.
Если $b = 7$ и $a \neq \frac{1}{2}$ является единственным решением
$x = \frac{2(7-1)}{2a-1} = \frac{12}{2a-1}$
Если a целое число, тогда $2a - 1$ также есть целым числом и решением есть
$x = \frac{12}{2a-1}$ является натуральным числом когда
$2a - 1$ есть положительным делителем для числа $12$.
Чтобы a было целым числом, делитель числа $12$ должен быть нечетным. Но только $1$ и $3$ являются положительными нечетными числами, на которые делится12
Поэтому $2a - 1 = 3 \Leftrightarrow a = 2$ или $2a - 1 = 1 \Leftrightarrow$
$a = 1 a = 2$ или $2a - 1 = 1 \Leftrightarrow a = 1$

Задача 7 Решите уравнение $|ax - 2 – a| = 4$, где a является параметром. Найдите, для каких значениях а корнями уравнения являются целые отрицательные числа.

Решение :

Из определения модуля мы получаем
$|ax - 2 – x| = 4 \Leftrightarrow ax - 2 – x = 4$ или $ax - 2 – x = - 4$
Из первого равенства мы получаем $x(a - 1) - 2 = 4 \Leftrightarrow$
$(a - 1)x = 4 + 2 \Leftrightarrow (a - 1)x = 6$
Из второго равенства мы получаем $(a - 1)x = -2$
Если $a - 1 = 0$, т.e. $a = 1$, последнее уравнение не имеет решения.
Если $a \neq 1$ мы находим, что $x = \frac{6}{a-1}$ или $x = -\frac{2}{a-1}$
Чтобы эти корни были целыми отрицательными числами, должно выполняться следующее:
Для первого равенство $a - 1$ должно быть отрицательным делителем 6, и для второго - положительным делителям 2
Тогда $a - 1 = -1; -2; -3; - 6$ или $a - 1 = 1; 2$
Мы получаем $a - 1 = -1 \Leftrightarrow a = 0; a - 1 = -2 \Leftrightarrow$
$a = -1; a - 1 = -3 \Leftrightarrow a = -2; a - 1 = -6 \Leftrightarrow a = -5$
или $a - 1 = 1 \Leftrightarrow a = 2; a - 1 = 2 \Leftrightarrow a = 3$
Тогда $a = -5; -2; -1; 0; 2; 3$ являются решениями задачи.

Задача 8 Решите уравнение:
A) $3ax – a = 1 – x$, где a это параметр;
B) $2ax + b = 2 + x$, где a и b являются параметрами

Решение :

A) $3ax + x = 1 + a \Leftrightarrow (3a + 1)x = 1 + a$.
Если $3a + 1 \neq 0$, т.e. $a \neq -11 /3 /3$ , решение есть
$x = \frac{1+a}{3a+1}$
Если $a = -\frac{1}{3}$ уравнение принимает вид $0\cdot x = \frac{1.1}{3}$, что не имеет решения.

B) $2ax – x = 2 – b \Leftrightarrow (2a - 1)x = 2 – b$
Если $2a - 1 \neq 0$, т.e. $a \neq \frac{1}{2}, x = \frac{2-b}{2a-1}$ является решением.
Если $a = \frac{1}{2}$ уравнение принимает вид $0.x = 2 – b$
Тогда, если $b = 2$, любое x является решением, если $b \neq 2$, уравнение не имеет решения.

Задача 9 Дано уравнение $6(kx - 6) + 24 = 5kx$ , где к - целое число. Найдите, для каких значений k уравнение:
A) имеет корень $-\frac{4}{3}$
B) не имеет решения;
C) имеет корень как натуральное число.

Решение :

Перепишем уравнение в виде $6kx - 36 + 24 = 5kx \Leftrightarrow kx = 12$

A) Если $x = -\frac{4}{3}$, для k мы получим уравнение $-\frac{4}{3k} = 12 \Leftrightarrow k = - 9$

B) Уравнение $kx = 12$ не имеет решения, когда $k = 0$

C) Когда $k \neq 0$ является корнем $x = \frac{12}{k}$ и это натуральное число, если k есть целым положительным числом, на которое делится 12, т.e. $k = 1, 2, 3, 4, 6, 12$

Задача 10 Решите уравнение:
A) $2ax + 1 = x + a$, где a является параметром;
B) $2ax + 1 = x + b$, где a и b являются параметрами.

Решение :

A) $2ax + 1 = x + a \Leftrightarrow 2ax – x = a - 1 \Leftrightarrow$
$(2a - 1)x = a - 1$
Если $2a - 1 \neq 0$, т.e. $a \neq \frac{1}{2}$, единственным решением уравнения является
$x = \frac{a-1}{2a-1}$
Если $2a - 1 = 0$, т.e. $a = \frac{1}{2}$, уравнение принимает вид
$0.x = \frac{1}{2}- 1 \Leftrightarrow 0.x = -\frac{1}{2}$, что не имеет решения

B) $2ax + 1 = x + b \Leftrightarrow$
$2ax – x = b - 1 \Leftrightarrow$
$(2a - 1)x = b - 1$
Если $2a - 1 \neq 0$, т.e. $a \neq \frac{1}{2}$, решением является
$x = \frac{b-1}{2a-1}$
Если $a = \frac{1}{2}$, уравнения эквивалентно $0.x = b - 1$
Если b = 1 любое x является решением, если $b \neq 1$ тогда нет решения.

Задача 11 Дано уравнение $3(ax - 4) + 4 = 2ax$, где параметром является целым числом. Найдите, для каких значений a уравнение в качестве корней имеет:
А) $\left(-\frac{2}{3}\right)$
B) целое число
C) натуральное число

Решение :

A) Если $x = -\frac{2}{3}$ есть решением уравнения, тогда должно быть истинным
$3\left + 4 = 2a\left(-\frac{2}{3}\right) \Leftrightarrow$
$-2a - 12 + 4 = -\frac{4a}{3} \Leftrightarrow$
$\frac{4a}{3} - 2a = 8 \Leftrightarrow \frac{4a-6a}{3} = 8 \Leftrightarrow$
$-\frac{2a}{3} = 8 \Leftrightarrow a = -12$

B) $3(ax - 4) + 4 = 2ax \Leftrightarrow 3ax - 2ax = 12 - 4 \Leftrightarrow ax = 8$
Если $a \neq 0$ решением является $x = \frac{8}{a}$, это целое число, если а является делимым числа $8$.
Поэтому; $±2; ±4; ±8$
Если $a=0$, уравнение не имеет решения

C) Чтобы получить натуральное (целое положительное) число для этого решения $x=\frac{8}{a}$ число должно равняться: $a=1, 2, 4, 8$

Задача 12 Дано уравнение $2 – x = 2b – 2ax$, где $a$ и $b$ - параметры. Найдите, для каких значений a уравнение имеет решения в виде натурального числа, если $b = 7$

Решение :

В уравнение мы подставляем $b = 7$ и получаем $2 – x = 2.7 - 2ax \Leftrightarrow$
$2ax – x = 14 – 2 \Leftrightarrow (2a - 1)x = 12$
Если $2a -1 \neq 0$, т.e. $a \neq \frac{1}{2}$, уравнение примет вид
$x = \frac{12}{2a-1}$ и это будет натуральное число, если знаменатель $2a - 1$ есть положительным делимым $12$ и кроме того, чтобы оно было целым числом, необходимо, чтобы $2a - 1$ было нечетным числом.
Поэтому $2a - 1$ может быть $1$ или $3$
Из $2a - 1 = 1 \Leftrightarrow 2a = 2 \Leftrightarrow a = 1$ и $2a - 1 = 3$
$\Leftrightarrow 2a = 4 \Leftrightarrow a = 2$

Задача 13 Дана функция $f(x) = (3a - 1)x - 2a + 1$, где a - параметр. Найдите, для каких значений a график функции:
А) пересекает ось абсцисс;
B) пересекает ось абсцисс

Решение :

Чтобы график функции пересёк ось абсцисс, необходимо, чтобы
$(3a - 1)\cdot x -2a + 1 = 0$ имело решения и не имело решения для непересечения оси абсцисс.
С уравнения мы получаем $(3a - 1)x = 2a - 1$
Если $3a - 1 \neq 0$, т.e. $a \neq \frac{1}{3}$, уравнение имеет решения
$x = \frac{2a-1}{3a-1}$, поэтому график функции пересекает ось абсцисс.
Если $a = \frac{1}{3}$, мы получаем $0.x = \frac{2}{3} - 1 \Leftrightarrow 0.x = -\frac{1}{3}$, что не имеет решения.
Поэтому, если $a = \frac{1}{3}$, график функций не пересекает ось абсцисс.

Задача 14 Решите параметрическое уравнение:
A) $|x -2| = a$
B) $|ax -1| = 3$
C) $|ax - 1| = a - 2$

Решение :

A) Если $a 0$ мы получаем:
$|x - 2| = a \Leftrightarrow x - 2 = a$ или $x - 2 = -a$
Из $x - 2 = a \Rightarrow x = a + 2$, и из
$x - 2 = -a \Rightarrow x = 2 – a$
Если $a = 0$, тогда $x - 2 = 0$ или $x = 2$

B) $|ax - 1| = 3 \Leftrightarrow ax - 1 = 3$ или $ax - 1 = -3$
откуда $ax = 4$ или $ax = - 2$
Если $a \neq 0$ решения: $x = \frac{4}{a}$ or $x = -\frac{2}{a}$
Если $a = 0$, здесь нет решения

C) Если $a - 2 Если $a - 2 > 0$, т.e. $a > 2$ мы получаем
$|ax - 1| = a - 2 \Leftrightarrow ax - 1 = a - 2$ или $ax - 1 = 2 – а$
Итак, мы получаем $ax = a - 1$ или $ax = 3 – a$
Потому что $a > 2, a \neq 0$, therefore
$x = \frac{a-1}{a}$ или $x = \frac{3-a}{a}$.
Если $a = 2$, уравнения эквивалентно
$2x - 1 = 0 \Leftrightarrow 2x = 1 \Leftrightarrow x = \frac{1}{2}$

Задача 15 Найдите, для каких значений параметра m (a), два уравнения эквивалентны:
A) $\frac{x+m}{2} = 1 – m$ и $(-x - 1) ^2 - 1 = x^2$
B) $\frac{x+m}{2} = 1 – m$ и $\frac{x-m}{3} = 1 - 2m$
C) $|3 – x| + x^2 -5x + 3 = 0$ и $ax + 2a = 1 + x$, если $x > 3$

Решение :

A) Решим второе уравнение. Запишем его в виде:
$(-x - 1)^2 - 1 = x^2 \Leftrightarrow$
$[(-1)(x + 1) ]^2 - 1 = x^2 \Leftrightarrow$
$x^2 + 2x + 1 - 1 = x^2 \Leftrightarrow$
$2x = 0 \Leftrightarrow x = 0$
Для первого мы получим
$\frac{x+m}{2} = 1 – m \Leftrightarrow x + m = 2 - 2m \Leftrightarrow x = 2 - 3m$
Эти два уравнения эквивалентны, если они имеют одинаковые корни, т.e.
$2 - 3m = 0 \Leftrightarrow$ $m = \frac{2}{3}$

B) Для первого уравнения решением есть $х = 2 - 3m$ и для второго мы получим
$x – m = 3 - 6m \Leftrightarrow$ $x = 3 – 5m$
Они имеют одинаковые корни, когда
$2 - 3m = 3 - 5m \Leftrightarrow 5m - 3m = 3 - 2 \Leftrightarrow 2m = 1 \Leftrightarrow m = \frac{1}{2}$

C) Так как $x > 3, 3 – x $|3 – x| = -(3 – x) = x - 3$
Первое уравнение будет выглядеть так: $x - 3 + x^2 – 5x + 3 = 0 \Leftrightarrow$
$x^2 - 4x – 0 \Leftrightarrow x(x - 4) = 0 \Leftrightarrow$
$x = 0$ или $x = 4$
С условием, что $х> 3$, поэтому только $x = 4$ есть решением. Для второго уравнения мы получаем
$ax – x = 1 - 2a \Leftrightarrow (a - 1)x = 1 - 2a$
Если $a - 1 = 0$, здесь нет решения (Почему?), если $a - 1 \neq 0$, i.e. $a \neq 1$, решением есть
$x = \frac{1-2a}{a-1}$ Эти два уравнения будут равны, если $4 = \frac{1-2a}{a-1} \Leftrightarrow$ $4(a - 1) = 1 - 2a \Leftrightarrow 4a + 2a = 1 + 4 \Leftrightarrow 6a = 5 \Leftrightarrow a = \frac{5}{6}$

1. Параметрическое уравнение прямой

Пусть даны точка M 0 (x 0 , y 0 , z 0 ) на прямой и вектор s = (l ,m ,n ) , лежащий на

этой прямой (или ей параллельной). Вектор s называют еще направляющим вектором прямой .

Этими условиями однозначно определяется прямая в пространстве. Найдем ее

уравнение. Возьмем произвольную точку M (x , y , z ) на прямой. Ясно, что векторы

M 0 M (x − x 0 , y − y 0 , z − z 0 ) и s коллинеарны.

Следовательно, M 0 M = t s − есть векторное уравнение прямой.

В координатной записи последнее уравнение имеет следующее параметрическое представление

двух углов, образованными двумя прямыми, соответственно параллельными данной и проходящими через одну точку (для чего возможно требуется совершить параллельный перенос одной из прямых).

Из определения следует, что один из углов равен углу ϕ между

Прямые перпендикулярны s 1 s 2 l 1 l 2 + m 1 m 2 + n 1 n 2 = 0 .

4. Угол между прямой и плоскостью. Условия « » и « » прямой и

плоскости

Пусть прямая L задана своим каноническим уравнением x − l x 0 = y − m y 0 = z − n z 0 ,

а плоскость P – уравнением

Ax + By + Cz + D = 0.

Определение. Углом между прямой L

и плоскостью р называется острый угол между прямой L и ее проекцией на плоскость.

Из определения (и рисунка) следует, что искомый угол ϕ является дополнительным (до прямого угла) к углу между вектором нормали n (A , B ,C ) и

направляющим вектором s (l ,m ,n ) .

(. берется, чтобы получить острый угол).

Если L Р , то тогда s n (s ,n ) = 0

Теперь, если подставить найденное «t » в параметрические уравнения прямой, то найдем искомую точку пересечения

Одной из основных операций математического анализа является операция предельного перехода, которая встречается в курсе в различных формах. Мы начнем с самой простейшей формы операции предельного перехода, основанной на понятии предела так называемой числовой последовательности. Это облегчит нам введение и другой весьма важной формы операции предельного перехода – предела функции. В последующем конструкции предельных переходов будут использоваться в построении дифференциального и интегрального исчисления.



 Бесконечно малые и бесконечно большие последовательности

 Связь бесконечно больших и бесконечно малых последовательностей.

 Простейшие свойства бесконечно малых последовательностей

 Предел последовательности.

 Свойства сходящихся последовательностей

 Арифметические операции над сходящимися последовательностями

 Монотонные последовательности

 Критерий сходимости Коши

 Число е и его экономическая иллюстрация.

 Применение пределов в экономических расчетах

§ 1. Числовые последовательности и простейшие свойства

1. Понятие числовой последовательности. Арифметические операции над последовательностями

Числовые последовательности представляют собой бесконечные множества чисел. Примеры последовательностей известны из школы:

1) последовательность всех членов бесконечной арифметической и геометрической прогрессий;

2) последовательность периметров правильных n -угольников, вписанных в данную окружность;

будем называть числовой последовательностью (или просто последовательностью).

Отдельные числа x 3 , x 5 , x n будем называть элементами или членами последовательности (1). Символ x n называют общим или n -м членом данной последовательности. Придавая значение n = 1, 2, … в общем члене x n мы получаем, соответственно, первый x 1 , второй x 2 и т.д. члены.

Последовательность считается заданной (см. Опр.), если указан способ получения любого ее элемента. Часто последовательность задают формулой для общего члена последовательности.

Для сокращения записи последовательность (1) иногда записывают как

Структура общего члена (его формула) может быть сложной. Например,

Иногда последовательность задается так называемыми рекуррентными формулами , т.е. формулами, позволяющими находить последующие члены последовательности по известным предыдущим.

Пример (числа Фибоначчи). Пусть x 1 = x 2 = 1 и задана рекуррентная формула x n = x n − 1 + x n − 2 для n = 3, 4, … . Тогда имеем последовательность 1, 1,

2, 3, 5, 8, … (числа Леонардо из Пизы по прозвищу Фибоначчи). Геометрически числовую последовательность можно изобразить на чис-

ловой оси в виде последовательности точек, координаты которых равны соот-

ветствующим членам последовательности. Например, { x n } = 1 n .

Лекция № 8-9 Основы математического анализа проф. Дымков М.П. 66

Рассмотрим наряду с последовательностью { x n } еще одну последовательность { y n } : y 1 , y 2 , y ,n (2).

Определение. Суммой (разностью, произведением, частным) последо-

вательностей { xn } и { yn } называется последовательность { zn } , члены кото-

Произведением последовательности { xn } на число c R называется последовательность { c xn } .

Определение. Последовательность { xn } называется ограниченной

сверху (снизу), если существует вещественное число М (m), такое что каждый элемент этой последовательности xn удовлетворяет неравен-

ству xn ≤ M (xn ≥ m) . Последовательность называется ограниченной, если она ограничена и сверху и снизу m ≤ xn ≤ M . Последовательность xn называ-

ется неограниченной, если для положительного числа А (сколь угодно большего) найдется хотя бы один элемент последовательности xn , удовлетворя-

ющий неравенству xn > A.

{ x n } = { 1n } − ограничена, т.к. 0 ≤ x n ≤ 1.

{ x n } = { n } − ограничена снизу 1, но является неограниченной.

{ x n } = { − n } − ограничена сверху (–1), но также неограниченная.

Определение. Последовательность { x n } называется бесконечно малой ,

если для любого положительного вещественного числа ε (сколь бы малым его не взяли) существует номер N , зависящий, вообще говоря от ε , (N = N (ε )) такой, что при всех n ≥ N выполняется неравенство x n < ε .

Пример. { x n } = 1 n .

Определение. Последовательность { xn } называется бесконечно боль-

шой , если для положительного вещественного числа А (какое бы большое оно не было) найдется номер N (N = N(A)) такой, что при всех n ≥ N выпол-

няется неравенство xn > A.

Одним из подпунктов темы «Уравнение прямой на плоскости» является вопрос составления параметрических уравнений прямой на плоскости в прямоугольной системе координат. В статье ниже рассматривается принцип составления подобных уравнений при определенных известных данных. Покажем, как от параметрических уравнений переходить к уравнениям иного вида; разберем решение типовых задач.

Конкретная прямая может быть определена, если задать точку, которая принадлежит этой прямой, и направляющий вектор прямой.

Допустим, нам задана прямоугольная система координат O x y . А также заданы прямая а с указанием лежащей на ней точки М 1 (x 1 , y 1) и направляющий вектор заданной прямой a → = (a x , a y) . Дадим описание заданной прямой a , используя уравнения.

Используем произвольную точку М (x , y) и получим вектор М 1 М → ; вычислим его координаты по координатам точек начала и конца: M 1 M → = (x - x 1 , y - y 1) . Опишем полученное: прямая задана множеством точек М (x , y) , проходит через точку М 1 (x 1 , y 1) и имеет направляющий вектор a → = (a x , a y) . Указанное множество задает прямую только тогда, когда векторы M 1 M → = (x - x 1 , y - y 1) и a → = (a x , a y) являются коллинеарными.

Существует необходимое и достаточное условие коллинеарности векторов, которое в данном случае для векторов M 1 M → = (x - x 1 , y - y 1) и a → = (a x , a y) возможно записать в виде уравнения:

M 1 M → = λ · a → , где λ – некоторое действительное число.

Определение 1

Уравнение M 1 M → = λ · a → называют векторно-параметрическим уравнением прямой.

В координатной форме оно имеет вид:

M 1 M → = λ · a → ⇔ x - x 1 = λ · a x y - y 1 = λ · a y ⇔ x = x 1 + a x · λ y = y 1 + a y · λ

Уравнения полученной системы x = x 1 + a x · λ y = y 1 + a y · λ носят название параметрических уравнений прямой на плоскости в прямоугольной системе координат. Суть названия в следующем: координаты всех точек прямой возможно определить по параметрическим уравнениям на плоскости вида x = x 1 + a x · λ y = y 1 + a y · λ при переборе всех действительных значений параметра λ

Согласно вышесказанному, параметрические уравнения прямой на плоскости x = x 1 + a x · λ y = y 1 + a y · λ определяют прямую линию, которая задана в прямоугольной системе координат, проходит через точку М 1 (x 1 , y 1) и имеет направляющий вектор a → = (a x , a y) . Следовательно, если заданы координаты некоторой точки прямой и координаты ее направляющего вектора, то возможно сразу записать параметрические уравнения заданной прямой.

Пример 1

Необходимо составить параметрические уравнения прямой на плоскости в прямоугольной системе координат, если заданы принадлежащая ей точка М 1 (2 , 3) и ее направляющий вектор a → = (3 , 1) .

Решение

На основе исходных данных получим: x 1 = 2 , y 1 = 3 , a x = 3 , a y = 1 . Параметрические уравнения будут иметь вид:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 2 + 3 · λ y = 3 + 1 · λ ⇔ x = 2 + 3 · λ y = 3 + λ

Наглядно проиллюстрируем:

Ответ: x = 2 + 3 · λ y = 3 + λ

Необходимо отметить: если вектор a → = (a x , a y) служит направляющим вектором прямой а, а точки М 1 (x 1 , y 1) и М 2 (x 2 , y 2) принадлежат этой прямой, то ее возможно определить, задав параметрическими уравнениями вида: x = x 1 + a x · λ y = y 1 + a y · λ , а также и таким вариантом: x = x 2 + a x · λ y = y 2 + a y · λ .

К примеру, нам заданы направляющий вектор прямой a → = (2 , - 1) , а также точки М 1 (1 , - 2) и М 2 (3 , - 3) , принадлежащие этой прямой. Тогда прямую определяют параметрические уравнения: x = 1 + 2 · λ y = - 2 - λ или x = 3 + 2 · λ y = - 3 - λ .

Следует обратить внимание и на такой факт: если a → = (a x , a y) - направляющий вектор прямой a , то ее направляющим векторомбудет и любой из векторов μ · a → = (μ · a x , μ · a y) , где μ ϵ R , μ ≠ 0 .

Таким образом, прямая а на плоскости в прямоугольной системе координат может быть определена параметрическими уравнениями: x = x 1 + μ · a x · λ y = y 1 + μ · a y · λ при любом значении μ , отличном от нуля.

Допустим, прямая а задана параметрическими уравнениями x = 3 + 2 · λ y = - 2 - 5 · λ . Тогда a → = (2 , - 5) - направляющий векторэтой прямой. А также любой из векторов μ · a → = (μ · 2 , μ · - 5) = 2 μ , - 5 μ , μ ∈ R , μ ≠ 0 станет направляющим вектором для заданной прямой. Для наглядности рассмотрим конкретный вектор - 2 · a → = (- 4 , 10) , ему соответствует значение μ = - 2 . В таком случае заданную прямую можно также определить параметрическими уравнениями x = 3 - 4 · λ y = - 2 + 10 · λ .

Переход от параметрических уравнений прямой на плоскости к прочим уравнениям заданной прямой и обратно

В решении некоторых задач применение параметрических уравнений является не самым оптимальным вариантом, тогда возникает необходимость перевода параметрических уравнений прямой в уравнения прямой другого вида. Рассмотрим, как же это сделать.

Параметрическим уравнениям прямой вида x = x 1 + a x · λ y = y 1 + a y · λ будет соответствовать каноническое уравнение прямой на плоскости x - x 1 a x = y - y 1 a y .

Разрешим каждое из параметрических уравнений относительно параметра λ , приравняем правые части полученных равенств и получим каноническое уравнение заданной прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y

При этом не должно смущать, если a x или a y будут равны нулю.

Пример 2

Необходимо осуществить переход от параметрических уравнений прямой x = 3 y = - 2 - 4 · λ к каноническому уравнению.

Решение

Запишем заданные параметрические уравнения в следующем виде: x = 3 + 0 · λ y = - 2 - 4 · λ

Выразим параметр λ в каждом из уравнений: x = 3 + 0 · λ y = - 2 - 4 · λ ⇔ λ = x - 3 0 λ = y + 2 - 4

Приравняем правые части системы уравнений и получим требуемое каноническое уравнение прямой на плоскости:

x - 3 0 = y + 2 - 4

Ответ: x - 3 0 = y + 2 - 4

В случае, когда необходимо записать уравнение прямой вида A x + B y + C = 0 , при этом заданы параметрические уравнения прямой на плоскости, необходимо сначала осуществить переход к каноническому уравнению, а затем к общему уравнению прямой. Запишем всю последовательность действий:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ λ = x - x 1 a x λ = y - y 1 a y ⇔ x - x 1 a x = y - y 1 a y ⇔ ⇔ a y · (x - x 1) = a x · (y - y 1) ⇔ A x + B y + C = 0

Пример 3

Необходимо записать общее уравнение прямой, если заданы определяющие ее параметрические уравнения: x = - 1 + 2 · λ y = - 3 · λ

Решение

Для начала осуществим переход к каноническому уравнению:

x = - 1 + 2 · λ y = - 3 · λ ⇔ λ = x + 1 2 λ = y - 3 ⇔ x + 1 2 = y - 3

Полученная пропорция идентична равенству - 3 · (x + 1) = 2 · y . Раскроем скобки и получим общее уравнение прямой: - 3 · x + 1 = 2 · y ⇔ 3 x + 2 y + 3 = 0 .

Ответ: 3 x + 2 y + 3 = 0

Следуя вышеуказанной логике действий, для получения уравнения прямой с угловым коэффициентом, уравнения прямой в отрезках или нормального уравнения прямой необходимо получить общее уравнение прямой, а от него осуществлять дальнейший переход.

Теперь рассмотрим обратное действие: запись параметрических уравнений прямой при другом заданном виде уравнений этой прямой.

Самый простой переход: от канонического уравнения к параметрическим. Пусть задано каноническое уравнение вида: x - x 1 a x = y - y 1 a y . Каждое из отношений этого равенства примем равным параметру λ:

x - x 1 a x = y - y 1 a y = λ ⇔ λ = x - x 1 a x λ = y - y 1 a y

Разрешим полученные уравнения относительно переменных x и y:

x = x 1 + a x · λ y = y 1 + a y · λ

Пример 4

Необходимо записать параметрические уравнения прямой, если известно каноническое уравнение прямой на плоскости: x - 2 5 = y - 2 2

Решение

Приравняем части известного уравнения к параметру λ: x - 2 5 = y - 2 2 = λ . Из полученного равенства получим параметрические уравнения прямой: x - 2 5 = y - 2 2 = λ ⇔ λ = x - 2 5 λ = y - 2 5 ⇔ x = 2 + 5 · λ y = 2 + 2 · λ

Ответ: x = 2 + 5 · λ y = 2 + 2 · λ

Когда необходимо осуществить переход к параметрическим уравнениям от заданного общего уравнения прямой, уравнения прямой с угловым коэффициентом или уравнения прямой в отрезках, необходимо исходное уравнение привести к каноническому, а после осуществлять переход к параметрическим уравнениям.

Пример 5

Необходимо записать параметрические уравнения прямой при известном общем уравнении этой прямой: 4 x - 3 y - 3 = 0 .

Решение

Заданное общее уравнение преобразуем в уравнение канонического вида:

4 x - 3 y - 3 = 0 ⇔ 4 x = 3 y + 3 ⇔ ⇔ 4 x = 3 y + 1 3 ⇔ x 3 = y + 1 3 4

Приравняем обе части равенства к параметру λ и получим требуемые параметрические уравнения прямой:

x 3 = y + 1 3 4 = λ ⇔ x 3 = λ y + 1 3 4 = λ ⇔ x = 3 · λ y = - 1 3 + 4 · λ

Ответ: x = 3 · λ y = - 1 3 + 4 · λ

Примеры и задачи с параметрическими уравнениями прямой на плоскости

Рассмотрим чаще всего встречаемые типы задач с использованием параметрических уравнений прямой на плоскости в прямоугольной системе координат.

1. В задачах первого типа заданы координаты точек, принадлежащих или нет прямой, описанной параметрическими уравнениями.

Решение таких задач опирается на следующий факт: числа (x , y) , определяемые из параметрических уравнений x = x 1 + a x · λ y = y 1 + a y · λ при некотором действительном значении λ , являются координатами точки, принадлежащей прямой, которая описывается этими параметрическими уравнениями.

Пример 6

Необходимо определить координаты точки, которая лежит на прямой, заданной параметрическими уравнениями x = 2 - 1 6 · λ y = - 1 + 2 · λ при λ = 3 .

Решение

Подставим в заданные параметрические уравнения известное значение λ = 3 и осуществим вычисление искомых координат: x = 2 - 1 6 · 3 y = - 1 + 2 · 3 ⇔ x = 1 1 2 y = 5

Ответ: 1 1 2 , 5

Также возможна следующая задача: пусть задана некоторая точка M 0 (x 0 , y 0) на плоскости в прямоугольной системе координат и нужно определить, принадлежит ли эта точка прямой, описываемой параметрическими уравнениями x = x 1 + a x · λ y = y 1 + a y · λ .

Чтобы решить подобную задачу, необходимо подставить координаты заданной точки в известные параметрические уравнения прямой. Если будет определено, что возможно такое значение параметра λ = λ 0 , при котором будут верными оба параметрических уравнения, тогда заданная точка является принадлежащей заданной прямой.

Пример 7

Заданы точки М 0 (4 , - 2) и N 0 (- 2 , 1) . Необходимо определить, являются ли они принадлежащими прямой, определенной параметрическими уравнениями x = 2 · λ y = - 1 - 1 2 · λ .

Решение

Подставим координаты точки М 0 (4 , - 2) в заданные параметрические уравнения:

4 = 2 · λ - 2 = - 1 - 1 2 · λ ⇔ λ = 2 λ = 2 ⇔ λ = 2

Делаем вывод, что точка М 0 принадлежит заданной прямой, т.к. соответствует значению λ = 2 .

2 = 2 · λ 1 = - 1 - 1 2 · λ ⇔ λ = - 1 λ = - 4

Очевидно, что не существует такого параметра λ , которому будет соответствовать точка N 0 . Другими словами, заданная прямая не проходит через точку N 0 (- 2 , 1) .

Ответ: точка М 0 принадлежит заданной прямой; точка N 0 не принадлежит заданной прямой.

1. В задачах второго типа требуется составить параметрические уравнения прямой на плоскости в прямоугольной системе координат. Самый простой пример такой задачи (при известных координатах точки прямой и направляющего вектора) был рассмотрен выше. Теперь разберем примеры, в которых сначала нужно найти координаты направляющего вектора, а потом записать параметрические уравнения.

Задана точка M 1 1 2 , 2 3 . Необходимо составить параметрические уравнения прямой, проходящей через эту точку и параллельной прямой x 2 = y - 3 - 1 .

Решение

По условию задачи прямая, уравнение которой нам предстоит опередить, параллельна прямой x 2 = y - 3 - 1 . Тогда в качестве направляющего вектора прямой, проходящей через заданную точку, возможно использовать направляющий вектор прямой x 2 = y - 3 - 1 , который запишем в виде: a → = (2 , - 1) . Теперь известны все необходимые данные для того, чтобы составить искомые параметрические уравнения:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 1 2 + 2 · λ y = 2 3 + (- 1) · λ ⇔ x = 1 2 + x · λ y = 2 3 - λ

Ответ: x = 1 2 + x · λ y = 2 3 - λ .

Пример 9

Задана точка М 1 (0 , - 7) . Необходимо записать параметрические уравнения прямой, проходящей через эту точку перпендикулярно прямой 3 x – 2 y – 5 = 0 .

Решение

В качестве направляющего вектора прямой, уравнение которой надо составить, возможно взять нормальный вектор прямой 3 x – 2 y – 5 = 0 . Его координаты (3 , - 2) . Запишем требуемые параметрические уравнения прямой:

x = x 1 + a x · λ y = y 1 + a y · λ ⇔ x = 0 + 3 · λ y = - 7 + (- 2) · λ ⇔ x = 3 · λ y = - 7 - 2 · λ

Ответ: x = 3 · λ y = - 7 - 2 · λ

1. В задачах третьего типа требуется осуществить переход от параметрических уравнений заданной прямой к прочим видам уравнений, которые ее определяют. Решение подобных примеров мы рассматривали выше, приведем еще один.

Дана прямая на плоскости в прямоугольной системе координат, определяемая параметрическими уравнениями x = 1 - 3 4 · λ y = - 1 + λ . Необходимо найти координаты какого-либо нормального вектора этой прямой.

Решение

Чтобы определить искомые координаты нормального вектора, осуществим переход от параметрических уравнений к общему уравнению:

x = 1 - 3 4 · λ y = - 1 + λ ⇔ λ = x - 1 - 3 4 λ = y + 1 1 ⇔ x - 1 - 3 4 = y + 1 1 ⇔ ⇔ 1 · x - 1 = - 3 4 · y + 1 ⇔ x + 3 4 y - 1 4 = 0

Коэффициенты переменных x и y дают нам требуемые координаты нормального вектора. Таким образом, нормальный вектор прямой x = 1 - 3 4 · λ y = - 1 + λ имеет координаты 1 , 3 4 .

Ответ: 1 , 3 4 .

Если вы заметили ошибку в тексте, пожалуйста, выделите её и нажмите Ctrl+Enter